X 2 2x 3 0
keralas
Sep 16, 2025 · 6 min read
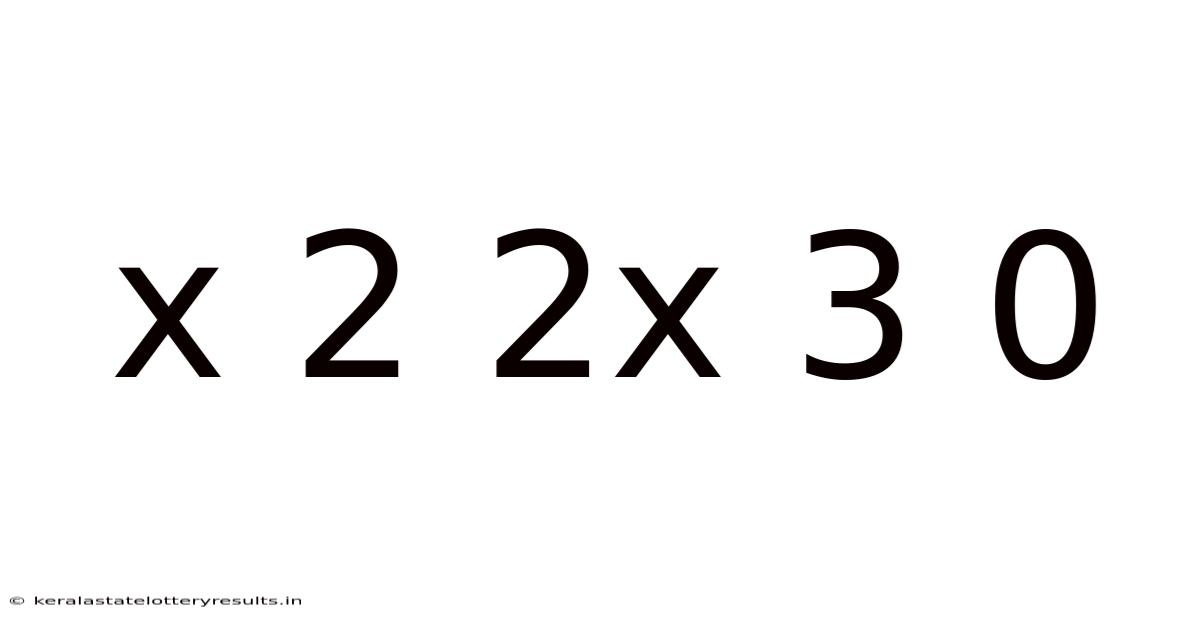
Table of Contents
Deconstructing the Mathematical Expression: x² + 2x + 3 = 0
This article delves into the mathematical expression x² + 2x + 3 = 0, exploring its nature, solving methods, and the broader context within algebra. We'll move beyond simply finding solutions and explore the underlying concepts, making this a comprehensive guide suitable for students and anyone interested in deepening their mathematical understanding. Understanding this seemingly simple equation unlocks a door to a wealth of mathematical concepts.
Introduction: Understanding Quadratic Equations
The equation x² + 2x + 3 = 0 is a quadratic equation. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (x in this case) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our specific equation, a = 1, b = 2, and c = 3.
Quadratic equations are fundamental to many areas of mathematics and science, appearing in applications ranging from physics (projectile motion) to economics (modeling growth and decay). Understanding how to solve them is a crucial skill for anyone pursuing further studies in STEM fields or related disciplines.
Methods for Solving Quadratic Equations
Several methods exist for solving quadratic equations. Let's explore the most common ones, applying them to our equation x² + 2x + 3 = 0.
1. Factoring: Factoring involves rewriting the quadratic expression as a product of two linear expressions. This method is only effective if the quadratic expression can be easily factored. Unfortunately, our equation x² + 2x + 3 = 0 cannot be factored using real numbers. Let's see why. We would need to find two numbers that add up to 2 (the coefficient of x) and multiply to 3 (the constant term). No such real numbers exist. This leads us to other methods.
2. Quadratic Formula: The quadratic formula is a powerful tool that works for all quadratic equations, regardless of whether they are factorable. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 2, c = 3), we get:
x = [-2 ± √(2² - 4 * 1 * 3)] / 2 * 1
x = [-2 ± √(4 - 12)] / 2
x = [-2 ± √(-8)] / 2
Notice the presence of √(-8). The square root of a negative number is an imaginary number. This means our equation has no real solutions.
3. Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's complete the square for our equation:
x² + 2x + 3 = 0
First, move the constant term to the right side:
x² + 2x = -3
Next, take half of the coefficient of x (which is 2), square it (1), and add it to both sides:
x² + 2x + 1 = -3 + 1
x² + 2x + 1 = -2
Now, the left side is a perfect square trinomial:
(x + 1)² = -2
Taking the square root of both sides:
x + 1 = ±√(-2)
x = -1 ± √(-2)
Again, we encounter imaginary numbers.
Understanding Complex Numbers and Imaginary Units
The appearance of √(-8) and √(-2) highlights the involvement of complex numbers. Complex numbers are numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit, defined as √(-1). In our solutions, we have:
-
For x = [-2 ± √(-8)] / 2: √(-8) = √(8)√(-1) = 2√(2)i. Therefore, x = -1 ± √(2)i
-
For x = -1 ± √(-2): This simplifies to x = -1 ± √(2)i.
Both methods yield the same complex solutions: x = -1 + √2i and x = -1 - √2i. These are conjugate pairs, a characteristic of quadratic equations with real coefficients.
Graphical Representation and the Discriminant
The nature of the solutions of a quadratic equation can be visualized graphically. The graph of a quadratic equation is a parabola. The parabola's intersection with the x-axis represents the real solutions of the equation. If the parabola does not intersect the x-axis, as in our case, the equation has no real solutions, only complex solutions.
The discriminant, denoted by Δ (delta), helps determine the nature of the solutions without actually solving the equation. The discriminant is the expression inside the square root in the quadratic formula: b² - 4ac.
- Δ > 0: Two distinct real solutions.
- Δ = 0: One real solution (a repeated root).
- Δ < 0: Two complex conjugate solutions.
In our equation, Δ = 2² - 4 * 1 * 3 = -8. Since Δ < 0, we confirmed that the equation has two complex conjugate solutions.
Applications of Quadratic Equations and Complex Numbers
While our specific equation may not directly model a real-world phenomenon using only real numbers, the underlying principles are crucial. Quadratic equations and complex numbers have numerous applications:
-
Physics: Describing projectile motion, oscillations, and wave phenomena often involves quadratic equations. Complex numbers are particularly useful in analyzing alternating current circuits and wave interference.
-
Engineering: In structural analysis, electrical engineering, and control systems, quadratic equations and complex numbers are essential tools for modeling and solving problems.
-
Signal Processing: Complex numbers are fundamental in representing and manipulating signals in the frequency domain, crucial for audio processing, image processing, and telecommunications.
-
Quantum Mechanics: Complex numbers are inherently integrated into the mathematical framework of quantum mechanics, describing wave functions and probabilities.
Frequently Asked Questions (FAQ)
Q: Why are complex numbers important?
A: Complex numbers extend the realm of numbers beyond the real numbers, enabling the solution of equations that have no real solutions and providing a more comprehensive mathematical framework for various applications in science and engineering.
Q: Can a quadratic equation have only one solution?
A: Yes, if the discriminant (b² - 4ac) is equal to 0, the quadratic equation has exactly one real solution, which is a repeated root.
Q: What is the difference between real and complex numbers?
A: Real numbers represent points on a number line, while complex numbers represent points on a complex plane, incorporating both real and imaginary components.
Q: Can I solve quadratic equations using a graphing calculator?
A: Yes, graphing calculators often have built-in functions to solve quadratic equations, providing both real and complex solutions.
Conclusion: Beyond the Solution
This exploration of the seemingly simple equation x² + 2x + 3 = 0 reveals a wealth of mathematical concepts. While the equation itself doesn't have real-world solutions in the context of real numbers, its solution highlights the importance of complex numbers and the power of various methods for solving quadratic equations. Understanding these methods and the underlying concepts is crucial for anyone pursuing further studies in mathematics, science, or engineering. The journey from a simple equation to a deeper understanding of complex numbers illustrates the beauty and interconnectedness of mathematical principles. Remember, even simple equations can hold profound mathematical insights when explored thoroughly.
Latest Posts
Latest Posts
-
Lcm Of 12 And 4
Sep 16, 2025
-
Sin 45 Degrees In Fraction
Sep 16, 2025
-
What Times What Equals 175
Sep 16, 2025
-
One Thousand And Fifty Dollars
Sep 16, 2025
-
3 4 Divided In Half
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 3 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.