X 2 2x 2 0
keralas
Sep 15, 2025 · 5 min read
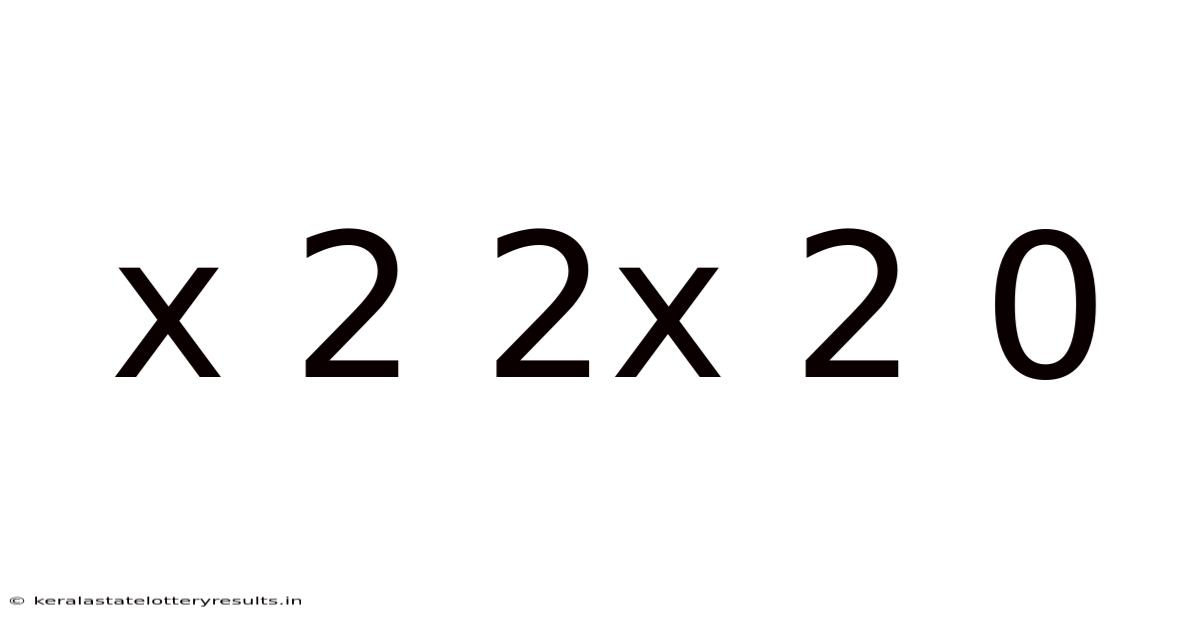
Table of Contents
Decoding the Enigma: A Deep Dive into x² + 2x + 2 = 0
This article explores the quadratic equation x² + 2x + 2 = 0, delving into its solution methods, underlying mathematical principles, and broader applications within algebra and beyond. We'll uncover not only the solutions themselves but also the significance of complex numbers and the general approach to solving quadratic equations. Understanding this seemingly simple equation reveals fundamental concepts that underpin much of higher mathematics.
Introduction: The Quadratic Equation and its Significance
Quadratic equations, equations of the form ax² + bx + c = 0 where a, b, and c are constants and a ≠ 0, are foundational elements of algebra. They represent a wide range of real-world problems, from calculating areas and trajectories to modeling growth and decay. The equation x² + 2x + 2 = 0, while appearing simple, serves as an excellent example to illustrate several key concepts in solving and interpreting quadratic solutions. This seemingly straightforward equation offers a gateway to understanding the intricacies of complex numbers and the power of different solution methods.
Methods for Solving x² + 2x + 2 = 0
Several approaches can be used to solve this quadratic equation. We'll examine two common methods: the quadratic formula and completing the square.
1. The Quadratic Formula: A Universal Solution
The quadratic formula provides a direct method for solving any quadratic equation. For the general equation ax² + bx + c = 0, the solutions are given by:
x = [-b ± √(b² - 4ac)] / 2a
In our specific case, x² + 2x + 2 = 0, we have a = 1, b = 2, and c = 2. Substituting these values into the quadratic formula, we get:
x = [-2 ± √(2² - 4 * 1 * 2)] / (2 * 1) x = [-2 ± √(4 - 8)] / 2 x = [-2 ± √(-4)] / 2
Notice the appearance of the square root of a negative number, √(-4). This signifies that the solutions to this equation are complex numbers.
2. Completing the Square: A Geometric Approach
Completing the square is a method that involves manipulating the equation to create a perfect square trinomial. This method provides a deeper understanding of the equation's structure.
Starting with x² + 2x + 2 = 0, we subtract 2 from both sides:
x² + 2x = -2
To complete the square, we take half of the coefficient of x (which is 2), square it (1), and add it to both sides:
x² + 2x + 1 = -2 + 1 x² + 2x + 1 = -1
Now, the left side is a perfect square trinomial: (x + 1)². So we have:
(x + 1)² = -1
Taking the square root of both sides:
x + 1 = ±√(-1)
Since √(-1) is defined as the imaginary unit i, we have:
x + 1 = ±i x = -1 ± i
Therefore, the solutions are x = -1 + i and x = -1 - i.
Understanding Complex Numbers: Beyond the Real
The solutions to x² + 2x + 2 = 0 involve complex numbers, numbers of the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit (√-1). Complex numbers extend the real number system, allowing us to solve equations that have no real solutions. In this case, the real part of both solutions is -1, and the imaginary parts are +i and -i respectively.
The Discriminant: Predicting the Nature of Solutions
The expression b² - 4ac within the quadratic formula is called the discriminant. It determines the nature of the solutions:
- b² - 4ac > 0: Two distinct real solutions.
- b² - 4ac = 0: One real solution (a repeated root).
- b² - 4ac < 0: Two complex conjugate solutions.
In our equation, b² - 4ac = 2² - 4 * 1 * 2 = -4 < 0. This confirms that the solutions are complex conjugates, as we found using both the quadratic formula and completing the square. Complex conjugate solutions always appear in pairs, with the imaginary part differing only in sign.
Graphical Representation: Visualizing Complex Solutions
While real solutions can be visualized as points on a number line, complex solutions require a different approach. The complex plane (also known as the Argand plane) is a two-dimensional coordinate system where the x-axis represents the real part and the y-axis represents the imaginary part of a complex number. The solutions -1 + i and -1 - i can be plotted as points in this plane.
Applications and Further Exploration
The seemingly abstract concept of complex numbers has profound applications in various fields:
- Electrical Engineering: Complex numbers are essential for analyzing alternating current (AC) circuits, where impedance and phase shifts are easily represented using complex numbers.
- Quantum Mechanics: Complex numbers play a crucial role in describing quantum states and wave functions.
- Signal Processing: Complex numbers are fundamental in representing and manipulating signals in various domains, like audio and image processing.
- Fluid Dynamics: Complex analysis provides powerful tools for solving problems related to fluid flow and potential theory.
Frequently Asked Questions (FAQ)
-
Q: Why are complex numbers important? A: Complex numbers extend the real number system, allowing us to solve equations that have no real solutions, and they have crucial applications in various scientific and engineering fields.
-
Q: What are complex conjugates? A: Complex conjugates are pairs of complex numbers with identical real parts and imaginary parts that differ only in sign (e.g., a + bi and a - bi). They often appear as solutions to quadratic equations with negative discriminants.
-
Q: Can I solve this equation using other methods? A: While the quadratic formula and completing the square are common, other methods, such as factoring (though not applicable here), could be used for different quadratic equations.
-
Q: What does the graphical representation of complex solutions tell us? A: The graphical representation on the complex plane helps visualize the location and relationship between complex solutions, which can be useful in understanding certain properties of the equation.
Conclusion: Bridging the Gap Between Theory and Application
The equation x² + 2x + 2 = 0, while seemingly simple, serves as a powerful illustration of key algebraic concepts. The process of solving it introduces us to complex numbers, a fundamental extension of the real number system with far-reaching implications in mathematics and numerous scientific disciplines. Understanding the various solution methods, the role of the discriminant, and the graphical representation of complex numbers provides a robust foundation for tackling more complex mathematical challenges. This deep dive highlights not only the "how" of solving the equation, but also the "why" it's significant, fostering a deeper appreciation for the beauty and utility of mathematics. It underscores the importance of embracing seemingly abstract concepts like complex numbers, as their practical applications extend far beyond the theoretical realm.
Latest Posts
Latest Posts
-
How Long Is 11 Cm
Sep 15, 2025
-
Multiplying Decimals By Whole Numbers
Sep 15, 2025
-
Integral Of 1 Sqrt X
Sep 15, 2025
-
93 Degrees Celsius To Fahrenheit
Sep 15, 2025
-
What Is 2 Of 100
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.