Whats Half Of 1 4
keralas
Sep 13, 2025 · 5 min read
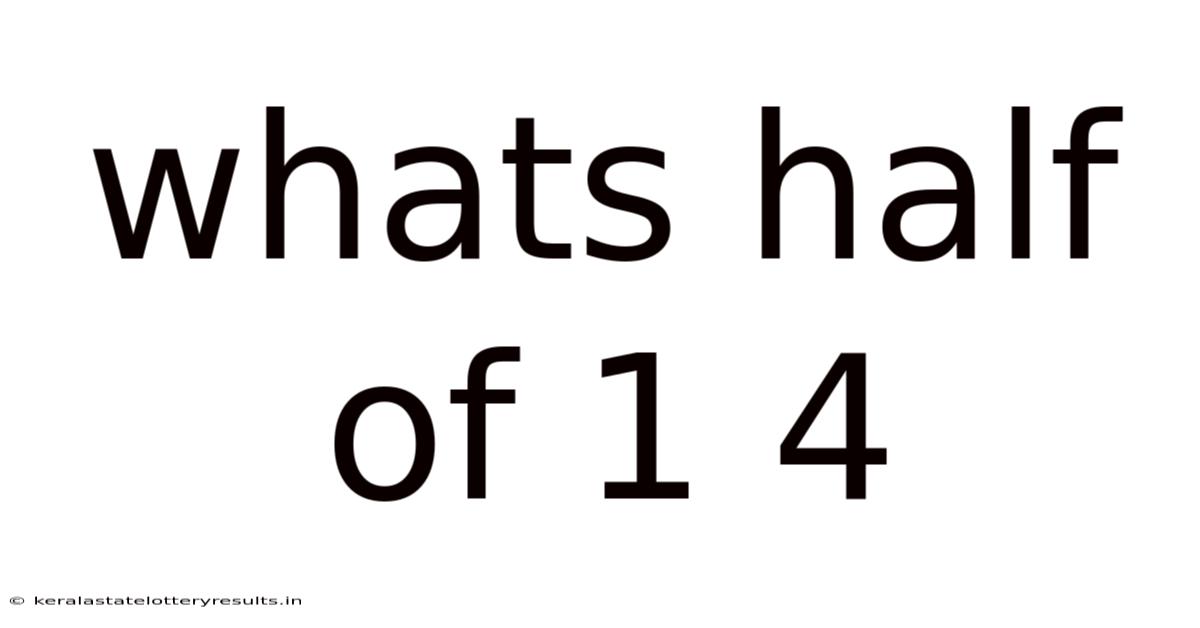
Table of Contents
What's Half of 1/4? A Deep Dive into Fractions and Division
What's half of 1/4? This seemingly simple question opens the door to a deeper understanding of fractions, division, and the fundamental principles of mathematics. While the answer itself is straightforward, exploring the why behind the solution provides valuable insight into mathematical concepts crucial for various levels of learning. This article will not only answer the question but also delve into the underlying principles, providing practical examples and addressing common misconceptions.
Understanding Fractions: The Building Blocks
Before tackling the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/4 (one-quarter), the numerator (1) tells us we have one part, and the denominator (4) tells us the whole is divided into four equal parts.
Finding Half of a Fraction: The Process
To find half of 1/4, we need to divide 1/4 by 2. There are two primary methods to approach this:
Method 1: Direct Division
We can express the problem as a division equation: (1/4) ÷ 2. Dividing a fraction by a whole number is the same as multiplying the fraction by the reciprocal of the whole number. The reciprocal of 2 is 1/2. Therefore:
(1/4) ÷ 2 = (1/4) × (1/2)
To multiply fractions, we multiply the numerators together and the denominators together:
(1 × 1) / (4 × 2) = 1/8
Therefore, half of 1/4 is 1/8.
Method 2: Visual Representation
Imagine a pizza cut into four equal slices. 1/4 represents one slice. To find half of that slice, you would cut that slice in half again. Now you have two smaller slices from the original quarter slice. The whole pizza is now divided into eight equal slices, and you have one of those eight slices (1/8). This visual representation reinforces the mathematical solution.
Extending the Concept: Halving Other Fractions
The method used to find half of 1/4 can be applied to other fractions. Let's explore a few examples:
- Half of 1/2: (1/2) ÷ 2 = (1/2) × (1/2) = 1/4
- Half of 2/3: (2/3) ÷ 2 = (2/3) × (1/2) = 2/6 = 1/3
- Half of 3/4: (3/4) ÷ 2 = (3/4) × (1/2) = 3/8
Notice the pattern: dividing a fraction by 2 effectively doubles the denominator.
Decimal Equivalents and Practical Applications
Understanding the decimal equivalent of fractions can be helpful. We can convert 1/4 to its decimal form by dividing the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25. Half of 0.25 is 0.125, which is the decimal equivalent of 1/8. This shows consistency across different mathematical representations.
In practical scenarios, understanding fractions is crucial in various fields:
- Cooking: Recipes often require fractional measurements. Knowing how to halve or double fractions is essential for adjusting recipes.
- Construction: Accurate measurements and calculations are critical in construction. Fractions are used extensively in blueprints and measurements.
- Finance: Understanding percentages (which are fractions expressed as parts of 100) is fundamental in finance for calculating interest, discounts, and profits.
Addressing Common Misconceptions
Some common misconceptions regarding fractions include:
- Incorrectly adding or subtracting fractions: Remember, you can only add or subtract fractions with the same denominator. If the denominators are different, you must find a common denominator before performing the operation.
- Misunderstanding reciprocals: The reciprocal of a number is simply 1 divided by that number. This is crucial when dividing fractions.
- Confusing multiplication and division: Remember the difference between multiplying and dividing fractions. Multiplication involves multiplying numerators and denominators, while division involves multiplying by the reciprocal.
Further Exploration: Beyond Halving
The concept of finding half extends to other divisions. For example, finding a third of 1/4 would involve dividing 1/4 by 3: (1/4) ÷ 3 = (1/4) × (1/3) = 1/12. Similarly, you can find any fraction of another fraction using the same principle of multiplying by the reciprocal.
This opens up a world of possibilities for exploring more complex fractional calculations and solidifying your understanding of fundamental mathematical operations.
Frequently Asked Questions (FAQ)
- Q: Can I always divide a fraction by another fraction? A: Yes, you can divide any fraction by any other fraction (as long as the divisor isn't zero). The process involves multiplying the first fraction by the reciprocal of the second fraction.
- Q: What if I need to find more than half? For example, what is 3/4 of 1/4? A: Simply multiply the fractions: (3/4) × (1/4) = 3/16
- Q: How can I simplify fractions after performing calculations? A: Simplify fractions by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. For instance, 2/6 can be simplified to 1/3 because the GCD of 2 and 6 is 2.
- Q: Why is it important to learn about fractions? A: Fractions are fundamental to many areas of mathematics and have practical applications in numerous real-world situations, from cooking and construction to finance and science. A solid grasp of fractions is essential for further mathematical learning.
Conclusion: Mastering Fractions, One Step at a Time
Finding half of 1/4, while seemingly trivial, provides a solid foundation for understanding fundamental mathematical principles. By exploring the underlying concepts of fractions, division, and reciprocal numbers, we not only find the answer (1/8) but also develop a deeper appreciation for the elegance and power of mathematics. This knowledge is transferable to more complex problems, making it a crucial building block for further mathematical learning and real-world problem-solving. Continue practicing with different fractions and operations to build your confidence and mastery of this essential mathematical skill. Remember that consistent practice and understanding the underlying principles are key to success in mathematics.
Latest Posts
Latest Posts
-
What Is 20 Off 120
Sep 13, 2025
-
What Are Factors Of 93
Sep 13, 2025
-
Gcf Of 20 And 25
Sep 13, 2025
-
Adjacent Angles Of A Parallelogram
Sep 13, 2025
-
Gcf Of 2 And 4
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Whats Half Of 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.