Whats 25 Percent Of 500
keralas
Sep 13, 2025 · 5 min read
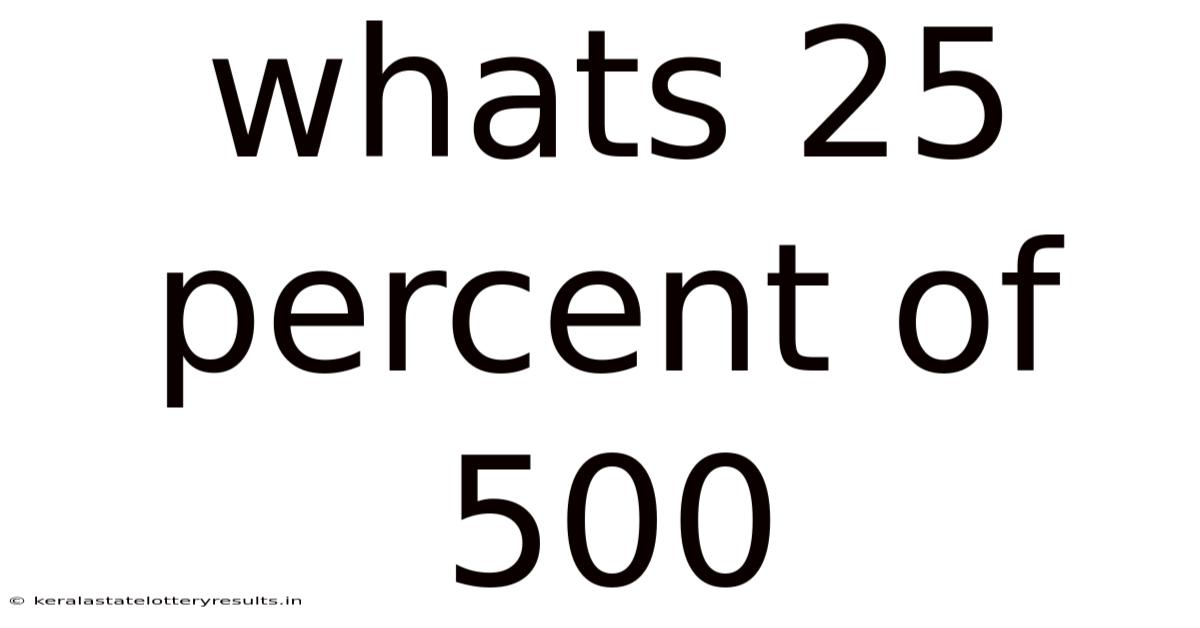
Table of Contents
What's 25 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 500 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a world of practical applications in various fields. This article will not only answer the question directly but also explore the concept of percentages, different methods for calculating them, and real-world examples showcasing their importance. We'll delve into the mathematical reasoning, address common misconceptions, and even touch upon advanced percentage calculations. By the end, you'll have a solid grasp of percentages and be able to confidently tackle similar problems.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This fundamental understanding is crucial for solving percentage problems.
Calculating 25% of 500: Three Methods
There are several ways to calculate 25% of 500. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As established, 25% is equal to 1/4. Therefore, finding 25% of 500 is the same as finding 1/4 of 500. This is a simple division:
500 / 4 = 125
Therefore, 25% of 500 is 125.
Method 2: Converting Percentage to Decimal
Another approach involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100:
25% / 100 = 0.25
Now, multiply this decimal by the number:
0.25 * 500 = 125
Again, we arrive at the answer: 125.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and their corresponding parts. We can set up a proportion:
25/100 = x/500
Where 'x' represents the unknown value (25% of 500). To solve for 'x', we cross-multiply:
25 * 500 = 100 * x
12500 = 100x
x = 12500 / 100
x = 125
Thus, using proportions, we confirm that 25% of 500 is 125.
Real-World Applications of Percentages
Percentages are ubiquitous in everyday life, appearing in various contexts:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. For example, understanding a 5% interest rate on a loan or a 20% discount on a purchase requires a firm grasp of percentage calculations.
-
Sales and Marketing: Analyzing market share, conversion rates, customer acquisition costs, and return on investment (ROI) for marketing campaigns. Tracking these metrics helps businesses make informed decisions about their strategies.
-
Science and Statistics: Representing data in charts and graphs, calculating probabilities, and expressing experimental results. Percentages provide a standardized way to compare and interpret data across various studies.
-
Education: Grading systems, test scores, and performance evaluations frequently utilize percentages. Understanding your percentage grade on an exam directly reflects your performance relative to the total possible score.
-
Everyday Life: Calculating tips in restaurants, determining the amount saved during sales, or figuring out nutritional information on food labels all involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 25% of 500 is relatively straightforward, more complex percentage problems may involve finding the percentage, the original value, or even dealing with multiple percentage changes.
Finding the Percentage: Let's say you scored 30 points out of a possible 50 points on a test. To find your percentage score, you would divide your score by the total possible score and multiply by 100:
(30 / 50) * 100 = 60%
Finding the Original Value: Imagine you bought an item on sale for $75 after a 25% discount. To find the original price, you can set up an equation:
Original Price - (25% of Original Price) = $75
Let 'x' represent the original price. Then:
x - 0.25x = 75
0.75x = 75
x = 75 / 0.75
x = $100
Therefore, the original price was $100.
Compound Percentages: These involve applying multiple percentage changes sequentially. For instance, if a price increases by 10% and then decreases by 10%, the final price will not be the same as the original price. This is because the second percentage change is applied to the new, increased price.
Percentage Increase/Decrease: To calculate the percentage increase or decrease between two values, follow these steps:
- Find the difference between the two values.
- Divide the difference by the original value.
- Multiply the result by 100 to express it as a percentage.
Common Misconceptions about Percentages
Several common misconceptions can lead to errors in percentage calculations:
-
Adding percentages directly: You cannot simply add percentages directly when dealing with multiple percentage changes. As shown in the compound percentage example, this will lead to inaccurate results.
-
Confusing percentage change with absolute change: A percentage change represents the relative change, while an absolute change represents the actual difference in value. It's crucial to distinguish between these two concepts.
-
Incorrectly interpreting percentage points: Percentage points represent the difference between two percentages, not the percentage change. For instance, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the initial 10%.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly in my head?
A: For common percentages like 10%, 25%, 50%, and 75%, you can use mental math techniques. For example, 10% is simply moving the decimal point one place to the left. 50% is halving the number. Practice will improve your speed and accuracy.
Q: Are there any online calculators or tools for calculating percentages?
A: Many online calculators and spreadsheet programs offer built-in functions for percentage calculations. These can be helpful for more complex problems or large datasets.
Q: What are some resources for learning more about percentages?
A: Numerous textbooks, online tutorials, and educational websites provide comprehensive coverage of percentages and related mathematical concepts.
Conclusion
Calculating 25% of 500, which equals 125, serves as a springboard for understanding the broader concept of percentages. Percentages are indispensable tools across numerous fields, requiring a thorough understanding of their calculation and application. This article aimed to provide a comprehensive guide, addressing different calculation methods, real-world applications, potential pitfalls, and frequently asked questions. Mastering percentages equips you with a valuable skillset applicable in various aspects of life, from personal finance to professional endeavors. Continuous practice and exploration of diverse problem types will further solidify your understanding and build confidence in tackling complex percentage calculations.
Latest Posts
Latest Posts
-
What Equals 48 In Multiplication
Sep 13, 2025
-
Area Of A Parallelogram Vectors
Sep 13, 2025
-
Factors Of 72 In Pairs
Sep 13, 2025
-
0 2 Repeating As A Fraction
Sep 13, 2025
-
5 4 5 As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.