What's 2 3 Of 6
keralas
Sep 13, 2025 · 5 min read
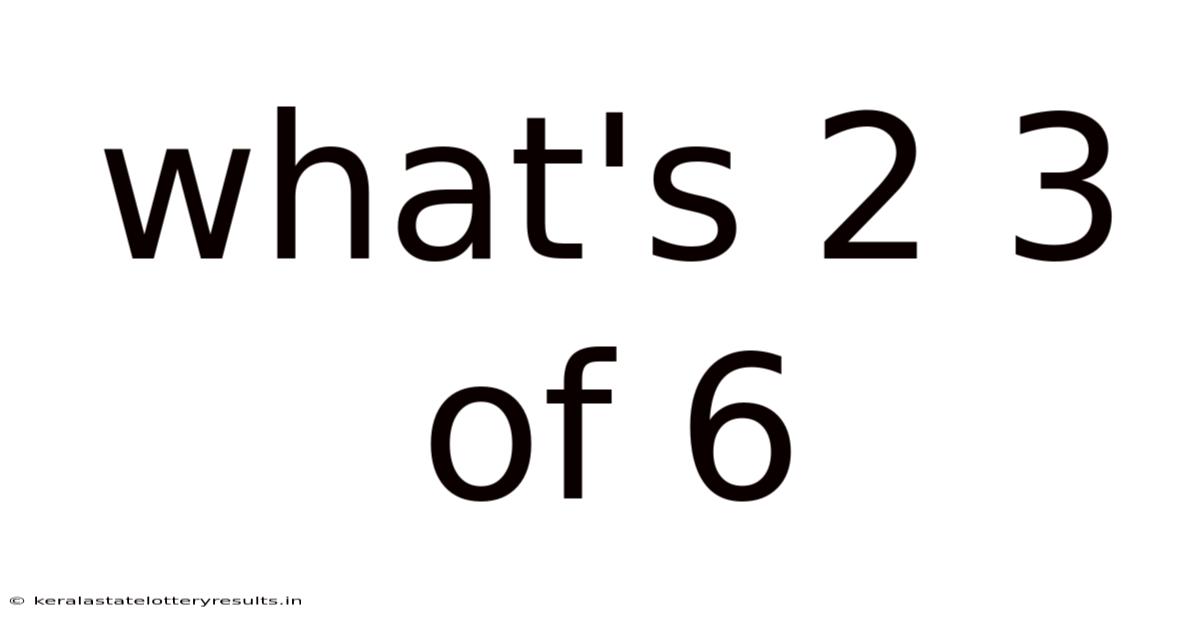
Table of Contents
What's 2/3 of 6? Understanding Fractions and Their Applications
Finding 2/3 of 6 might seem like a simple arithmetic problem, but it's a gateway to understanding fundamental concepts in mathematics, particularly fractions and their applications in everyday life. This article will delve deep into solving this problem, exploring the underlying principles, different methods of calculation, and demonstrating its relevance in various contexts. We'll also tackle some frequently asked questions and explore related concepts to provide a comprehensive understanding.
Introduction: Fractions – The Building Blocks of Mathematics
Fractions represent parts of a whole. They are expressed as a ratio of two numbers, the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering. In our case, 2/3 means two out of three equal parts. Understanding fractions is crucial for various aspects of life, from cooking and sewing to finance and engineering.
Method 1: Direct Calculation – Multiplying Fractions
The most straightforward way to find 2/3 of 6 is to multiply the fraction by the whole number. We can express 6 as a fraction, 6/1. The calculation is then:
(2/3) * (6/1) = (2 * 6) / (3 * 1) = 12/3 = 4
Therefore, 2/3 of 6 is 4. This method highlights the fundamental principle of multiplying fractions: multiply the numerators together and the denominators together.
Method 2: Dividing and Multiplying – A Step-by-Step Approach
This method breaks down the process into two simpler steps:
-
Divide by the denominator: Divide 6 by the denominator of the fraction (3). 6 / 3 = 2. This gives us the size of one-third of 6.
-
Multiply by the numerator: Multiply the result from step 1 by the numerator of the fraction (2). 2 * 2 = 4. This gives us the size of two-thirds of 6.
This method is particularly helpful for visualizing the problem. It clarifies that we first find the size of one-third, and then we multiply to find the size of two-thirds.
Method 3: Visual Representation – Understanding Fractions Geometrically
Let's imagine a rectangle divided into three equal parts. Each part represents 1/3 of the whole. If the whole rectangle represents 6, then each part represents 6/3 = 2. Since we want 2/3, we shade two of these parts. The shaded area represents 2 * 2 = 4. This visual method makes the concept of fractions more intuitive, particularly for beginners.
Real-World Applications: Where Fractions Matter
The seemingly simple calculation of 2/3 of 6 has widespread applications in various fields:
-
Cooking and Baking: Recipes often use fractions to specify ingredient quantities. For instance, a recipe might call for 2/3 cup of sugar.
-
Construction and Engineering: Precise measurements are essential in these fields. Fractions are used extensively in blueprints and calculations to ensure accuracy.
-
Finance and Budgeting: Understanding fractions is crucial for calculating percentages, discounts, interest rates, and proportions of budgets.
-
Data Analysis: In statistics and data analysis, fractions are used to represent proportions and probabilities.
-
Everyday Life: Sharing items equally, calculating discounts, or determining proportions often involves fractional calculations.
Expanding the Concept: Working with Different Fractions and Whole Numbers
The principles discussed above can be applied to any fraction and whole number. For example, let's find 3/4 of 12:
(3/4) * (12/1) = (3 * 12) / (4 * 1) = 36/4 = 9
Or, let's find 5/8 of 24:
(5/8) * (24/1) = (5 * 24) / (8 * 1) = 120/8 = 15
These examples demonstrate that the same methods—direct multiplication or dividing and multiplying—can be used to solve a wide range of fraction problems.
Beyond Simple Fractions: Dealing with Improper Fractions and Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4). A mixed number combines a whole number and a fraction (e.g., 1 ¾). While our example uses a simple proper fraction, it's important to understand how to handle other types of fractions.
To find a fraction of a whole number involving improper fractions or mixed numbers, first convert the mixed number into an improper fraction. Then, perform the multiplication as described previously. For instance, to find 1 ½ of 6:
First, convert 1 ½ to an improper fraction: 1 ½ = (1 * 2 + 1) / 2 = 3/2
Then, perform the multiplication: (3/2) * (6/1) = 18/2 = 9
Frequently Asked Questions (FAQs)
-
Q: What if the whole number isn't divisible by the denominator? A: You'll still perform the multiplication as usual. The result might be a fraction or a mixed number. For example, 2/3 of 7 is (2/3) * (7/1) = 14/3 = 4 ⅔.
-
Q: Can I use a calculator to solve these problems? A: Absolutely! Calculators are helpful for more complex fraction calculations.
-
Q: Are there other ways to visualize fractions? A: Yes, circles, pie charts, and other shapes can also be used to visualize fractions effectively.
-
Q: How can I improve my understanding of fractions? A: Practice is key! Work through different problems, use visual aids, and seek help when needed.
Conclusion: Mastering Fractions – A Foundation for Future Learning
Understanding how to find 2/3 of 6, and more generally how to work with fractions, is a crucial building block for success in mathematics and beyond. The ability to perform these calculations efficiently and accurately is essential in various fields and everyday situations. By mastering these fundamental concepts, you equip yourself with valuable skills applicable across many areas of life, from everyday budgeting to complex engineering calculations. This simple problem unlocks a world of mathematical understanding, highlighting the elegance and practicality of fractions. Remember to practice regularly and explore different methods to solidify your understanding and build confidence in tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
Factors Of 147 In Pairs
Sep 14, 2025
-
80 Percent To A Fraction
Sep 14, 2025
-
How To Multiply 2 Vectors
Sep 14, 2025
-
Is 21 Odd Or Even
Sep 14, 2025
-
Whats 37 Celsius In Fahrenheit
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What's 2 3 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.