What Times What Equals 77
keralas
Sep 15, 2025 · 5 min read
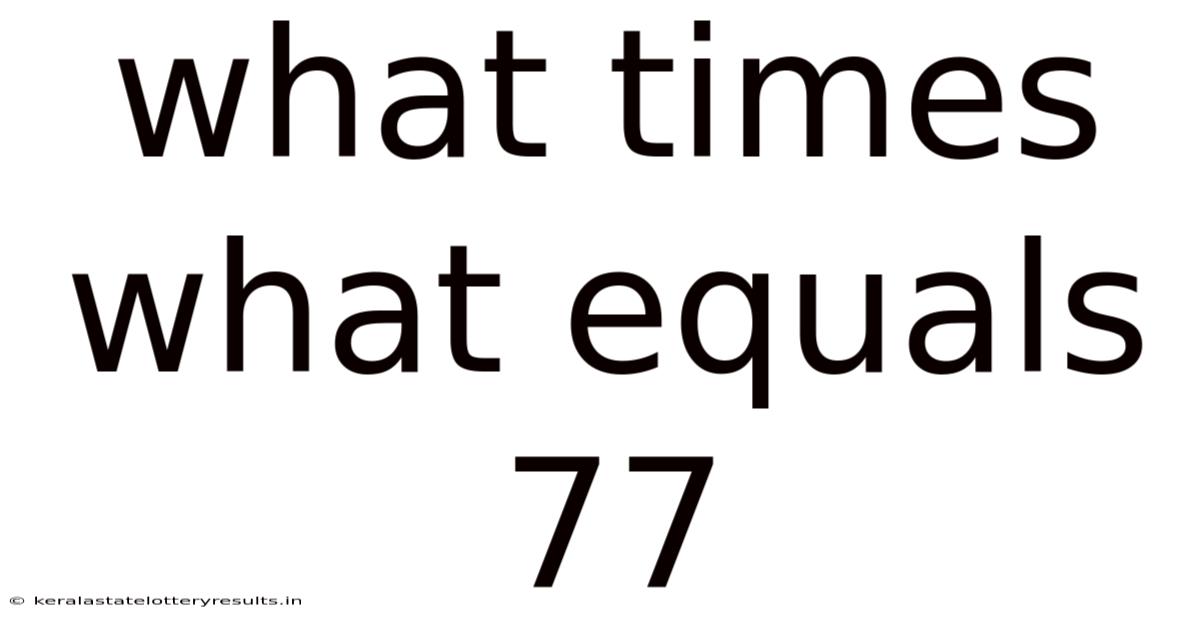
Table of Contents
Unraveling the Mystery: What Times What Equals 77? A Deep Dive into Factorization and Number Theory
Finding the factors of a number, a seemingly simple arithmetic task, opens a door to a fascinating world of mathematics. This article delves into the question "What times what equals 77?" exploring not just the immediate answer but the broader mathematical concepts involved, including factorization, prime numbers, and their significance in number theory. We'll examine different approaches to solving this problem and uncover the underlying principles that make it more than just a simple multiplication puzzle.
Understanding Factorization: The Building Blocks of Numbers
Factorization is the process of breaking down a number into smaller numbers that, when multiplied together, give the original number. These smaller numbers are called factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because 1 x 12 = 12, 2 x 6 = 12, and 3 x 4 = 12. Finding the factors of a number helps us understand its structure and properties.
In the case of 77, we're looking for two numbers (or potentially more, depending on how we approach the problem) that, when multiplied, result in 77. This seemingly simple question touches upon fundamental concepts within number theory.
Finding the Factors of 77: A Step-by-Step Approach
The most straightforward approach to finding the factors of 77 is to systematically test different pairs of numbers. We can start by considering small numbers and gradually increase them until we find a pair that works:
- 1 x 77 = 77: This is the trivial factorization, always present for any number.
- 7 x 11 = 77: This is the non-trivial factorization and represents the prime factorization of 77.
Therefore, the answer to "What times what equals 77?" is 7 times 11. These are the only two whole numbers that satisfy this equation.
Prime Numbers and the Uniqueness of Prime Factorization
The fact that 7 and 11 are the only whole number factors of 77 highlights the importance of prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. 7 and 11 are both prime numbers. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This means there's only one way to factorize a number into its prime components, regardless of the order. This unique prime factorization is a cornerstone of number theory. For 77, its prime factorization is simply 7 x 11.
Beyond the Basics: Exploring Other Mathematical Concepts
The simple question of "What times what equals 77?" opens avenues to explore more complex mathematical ideas:
-
Greatest Common Divisor (GCD): The GCD of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. Since 7 and 11 are prime and have no common factors other than 1, their GCD is 1. This means they are relatively prime or coprime.
-
Least Common Multiple (LCM): The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. The LCM of 7 and 11 is 77, which is also their product because they are coprime. If the numbers weren't coprime, the LCM would be smaller than their product.
-
Modular Arithmetic: Modular arithmetic deals with remainders after division. For example, 77 modulo 7 is 0 (77 divided by 7 leaves a remainder of 0), and 77 modulo 11 is also 0. Understanding modular arithmetic is crucial in various fields like cryptography and computer science.
-
Divisibility Rules: While trial and error works for smaller numbers, understanding divisibility rules can expedite the process for larger numbers. There aren't specific divisibility rules for 77, but understanding divisibility by 7 and 11 individually helps in finding factors of numbers potentially divisible by 77.
Applications of Factorization: Real-World Significance
Factorization, while seemingly abstract, has significant real-world applications:
-
Cryptography: The security of many encryption algorithms relies on the difficulty of factoring large numbers into their prime components. Breaking these codes often involves finding the prime factors of incredibly large numbers, a task that becomes computationally expensive as the numbers grow.
-
Coding Theory: Error correction codes, crucial for reliable data transmission, often utilize concepts related to prime numbers and factorization.
-
Computer Science: Algorithms in computer science frequently rely on factorization for optimization and efficient processing of data.
Frequently Asked Questions (FAQ)
-
Q: Are there any other ways to find the factors of 77 besides trial and error?
A: While trial and error is the most intuitive method for small numbers, more sophisticated algorithms exist for larger numbers. These algorithms are vital in cryptography and computational number theory. However, for 77, trial and error is perfectly efficient.
-
Q: Why are prime numbers important in factorization?
A: Prime numbers are the building blocks of all integers. The Fundamental Theorem of Arithmetic guarantees that every integer greater than 1 has a unique prime factorization. This uniqueness is essential in many mathematical proofs and applications.
-
Q: What if the question was "What times what equals a different number?"
A: The same principles apply. You would need to find the factors of that number. For larger numbers, systematic approaches and potentially specialized algorithms would be necessary.
-
Q: Can negative numbers be factors?
A: Yes. While we typically focus on positive factors, -7 x -11 = 77 is also a valid factorization. This expands the number of factor pairs to include negative values.
Conclusion: Beyond the Simple Answer
The seemingly straightforward question, "What times what equals 77?", leads us down a path that explores fundamental concepts in number theory, highlighting the importance of factorization, prime numbers, and their significant role in various fields. While the answer is simply 7 x 11 (and -7 x -11), understanding the underlying mathematical principles enriches our understanding of numbers and their inherent properties, expanding beyond a simple arithmetic solution. The journey of uncovering the factors of 77 offers a glimpse into the rich tapestry of mathematics and its profound influence on our world.
Latest Posts
Latest Posts
-
Square Root Of 7 Irrational
Sep 15, 2025
-
Factors Of 288 In Pairs
Sep 15, 2025
-
Line Parallel To X Axis
Sep 15, 2025
-
Is 413 A Prime Number
Sep 15, 2025
-
20 By 20 Multiplication Chart
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 77 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.