What Times What Equals 35
keralas
Sep 15, 2025 · 6 min read
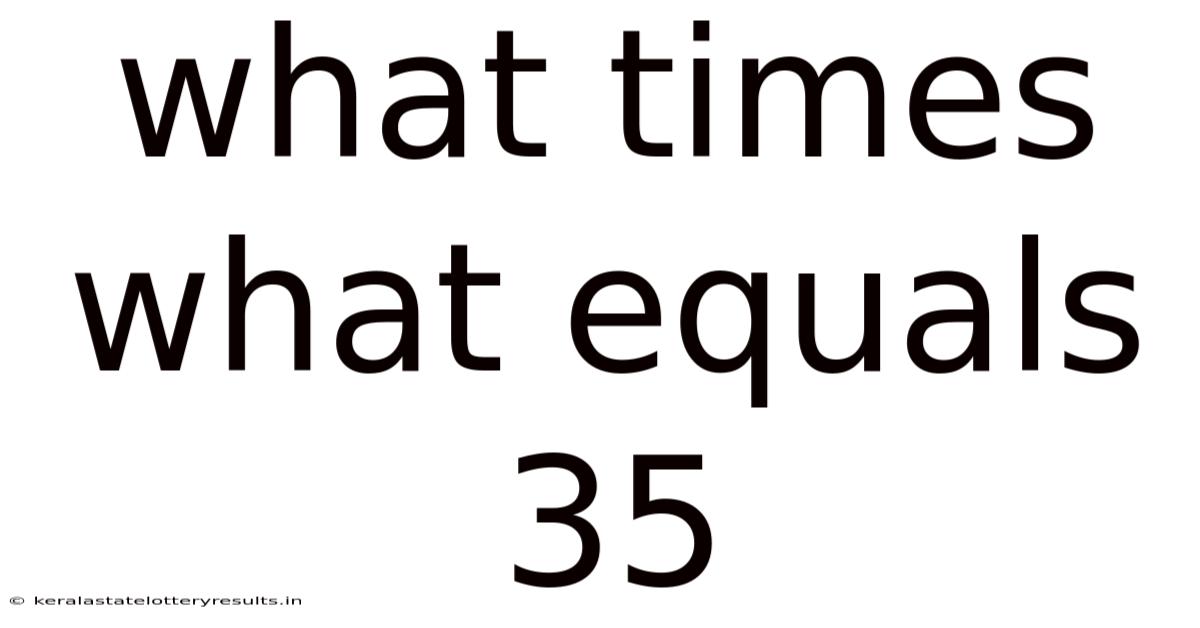
Table of Contents
What Times What Equals 35? Exploring the Factors and Applications of Multiplication
Finding the numbers that, when multiplied, result in 35 might seem like a simple arithmetic problem. However, delving deeper reveals interesting concepts within number theory, prime factorization, and even practical applications in various fields. This article will explore the different ways to approach this seemingly basic question, moving beyond the immediate answer to uncover the underlying mathematical principles and real-world relevance.
Understanding the Fundamentals: Factors and Prime Numbers
The core of this problem lies in understanding factors. Factors are numbers that divide evenly into a larger number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. To find what numbers multiplied together equal 35, we're essentially looking for the factor pairs of 35.
The process of finding these factor pairs is made easier by considering prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Prime factorization is the process of expressing a number as a product of its prime factors.
Let's apply this to 35:
- Is 35 divisible by 2? No, it's an odd number.
- Is 35 divisible by 3? No, the sum of its digits (3 + 5 = 8) is not divisible by 3.
- Is 35 divisible by 5? Yes, 35 / 5 = 7.
- Is 7 a prime number? Yes.
Therefore, the prime factorization of 35 is 5 x 7. This means the only whole number factor pairs of 35 are 1 x 35 and 5 x 7. If we expand to include negative numbers, we also have -1 x -35 and -5 x -7.
Beyond Whole Numbers: Exploring Rational and Irrational Factors
While the whole number factor pairs are straightforward, the question opens up possibilities when considering other number systems. We can explore rational and irrational numbers.
-
Rational Numbers: Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Infinitely many rational numbers, when multiplied, can result in 35. For example: (10/2) * 7 = 35, (35/10) * 10 = 35, and so on. The possibilities are limitless.
-
Irrational Numbers: Irrational numbers cannot be expressed as a simple fraction. Numbers like π (pi) and the square root of 2 are irrational. While it's less intuitive, it's mathematically possible to find irrational numbers that, when multiplied, equal 35. This often involves manipulating equations and using more advanced mathematical techniques. For instance, you could set up an equation where one irrational number is defined in relation to 35 and another is defined to compensate for that irrationality, ultimately resulting in their product being 35.
Practical Applications of Factorization and Multiplication
The seemingly simple problem of finding numbers that multiply to 35 has surprising real-world applications:
-
Algebra: Factorization is a crucial skill in algebra for solving equations and simplifying expressions. Understanding factors helps in factoring quadratic equations, which are used extensively in physics, engineering, and economics to model various phenomena.
-
Geometry: Calculating areas and volumes frequently involves multiplication. For instance, if a rectangle has a length of 5 units and a width of 7 units, its area is 35 square units. This extends to three-dimensional shapes where the volume is calculated by multiplying three dimensions.
-
Computer Science: Factorization plays a vital role in cryptography, specifically in RSA encryption. RSA relies on the difficulty of factoring large numbers into their prime factors to secure online transactions and data. While 35 is easily factored, the principle extends to much larger numbers, making it the basis of secure communication on the internet.
-
Everyday Life: Even in everyday situations, the concept is applied. If you need to buy 7 packs of pencils with 5 pencils per pack, you'll have a total of 35 pencils. This simple example highlights how fundamental multiplication and factorization are in our daily lives.
Advanced Mathematical Concepts: Beyond Basic Factorization
The concept extends beyond simple factor pairs. Let's consider some advanced mathematical perspectives:
-
Modular Arithmetic: In modular arithmetic, we are interested in the remainder when a number is divided by a particular modulus. For example, in modulo 10 arithmetic, 35 is equivalent to 5 (35 divided by 10 leaves a remainder of 5). This has applications in cryptography and other areas.
-
Complex Numbers: Complex numbers are numbers that consist of a real part and an imaginary part, involving the imaginary unit 'i', where i² = -1. While it's possible to find complex numbers whose product is 35, this involves more advanced algebraic manipulation.
-
Number Theory: Number theory is a branch of mathematics dedicated to studying the properties of integers. The quest to understand numbers like 35, their factors, and their relationships with other numbers contributes to a broader understanding of fundamental mathematical structures and patterns.
Frequently Asked Questions (FAQ)
-
Q: Are there any other numbers that, when multiplied, equal 35 besides 5 and 7? A: Within the realm of whole numbers, only 1 and 35, and their negative counterparts (-1 and -35, -5 and -7) provide whole number solutions. However, infinitely many rational and irrational numbers can also produce 35 when multiplied.
-
Q: How is this concept used in real-world problem-solving? A: As discussed above, factorization and multiplication are crucial in algebra, geometry, computer science (especially cryptography), and countless everyday calculations. It's the foundational base for many complex mathematical problems.
-
Q: Is there a limit to the number of combinations of numbers that can multiply to 35? A: No, there is no limit if we extend beyond whole numbers to include rational and irrational numbers. The possibilities become infinite.
-
Q: What if I wanted to find numbers that multiply to a different number, say 100? A: The same principles apply. You would find the prime factorization of 100 (2 x 2 x 5 x 5) and then identify all possible combinations of factors that multiply to 100.
Conclusion: The Richness of a Simple Question
The seemingly simple question of "what times what equals 35?" opens a window into a fascinating world of mathematical concepts. From basic arithmetic and prime factorization to advanced applications in algebra, geometry, computer science, and number theory, this question highlights the interconnectedness of various mathematical fields and their relevance to the real world. It demonstrates that even the most fundamental mathematical operations can unlock a deep and rewarding exploration of mathematical principles and their practical applications. The seemingly straightforward answer – 5 x 7 – represents only the starting point of a much larger and richer mathematical journey.
Latest Posts
Latest Posts
-
Formula For Right Triangle Perimeter
Sep 15, 2025
-
How Far Is 30 Yards
Sep 15, 2025
-
What Is 4 5 Equivalent To
Sep 15, 2025
-
Sum Of Even Numbers Formula
Sep 15, 2025
-
Is 299 A Prime Number
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.