What Times What Equals 15
keralas
Sep 14, 2025 · 6 min read
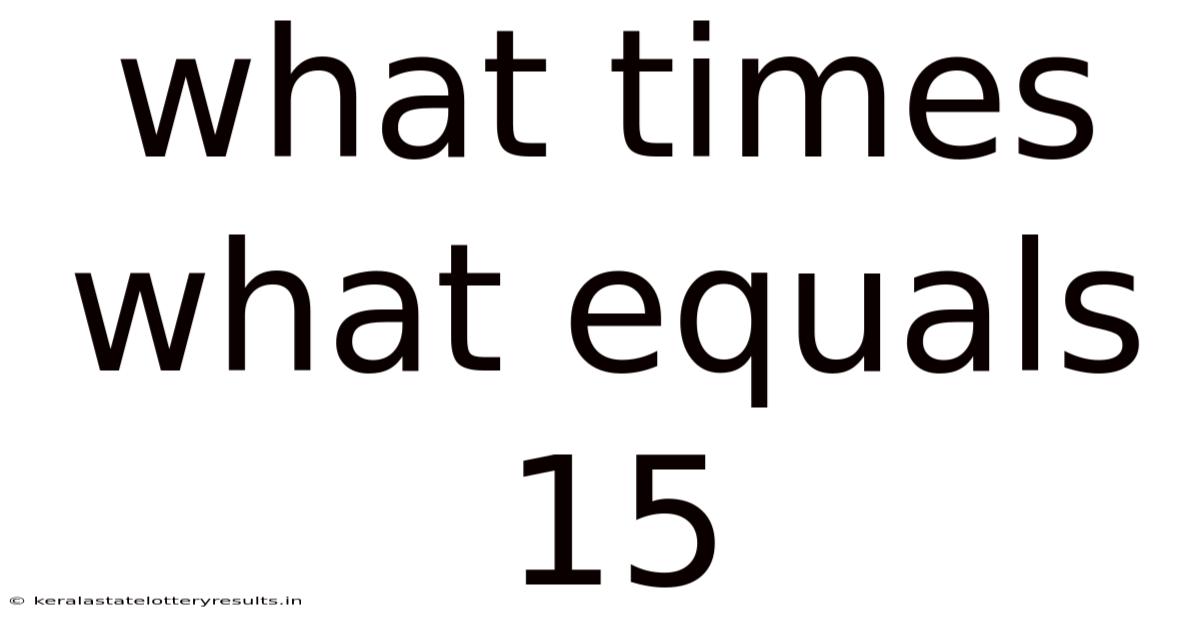
Table of Contents
What Times What Equals 15? Exploring the Factors and Applications of Fifteen
Finding the numbers that multiply to equal 15 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly basic question opens the door to a deeper exploration of factors, prime numbers, and even algebraic concepts. This article delves into the various ways to arrive at the answer, explores the mathematical properties involved, and expands on the practical applications of understanding factor pairs. We'll move beyond just the simple answer and uncover the richer mathematical landscape hidden within this seemingly straightforward equation.
Understanding Factors and Factor Pairs
Before we dive into the specific solutions for "what times what equals 15," let's clarify the fundamental concept of factors. Factors are whole numbers that divide evenly into a larger number without leaving a remainder. In other words, they are numbers that can be multiplied together to produce a specific product. A factor pair is a set of two factors that, when multiplied, result in the target number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Some factor pairs of 12 are (1, 12), (2, 6), and (3, 4).
Finding the Factor Pairs of 15
Now, let's apply this concept to the number 15. What are the whole numbers that, when multiplied together, equal 15? The factor pairs are:
- (1, 15): 1 multiplied by 15 equals 15.
- (3, 5): 3 multiplied by 5 equals 15.
These are all the whole number factor pairs for 15. It's important to note that we are considering only positive whole numbers here. If we included negative numbers, we would also have (-1, -15) and (-3, -5) as factor pairs, since a negative number multiplied by a negative number results in a positive number.
The Significance of Prime Numbers
The number 15 is considered a composite number because it has factors other than 1 and itself. This is in contrast to a prime number, which is a whole number greater than 1 that has only two factors: 1 and itself. The prime numbers less than 15 are 2, 3, 5, 7, 11, and 13.
Understanding the prime factorization of a number is crucial in many areas of mathematics. The prime factorization of 15 is 3 x 5. This means that 15 can be expressed as the product of only its prime factors. This seemingly simple concept is fundamental to more advanced mathematical operations, including finding the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers.
Expanding the Concept: Algebraic Equations
The question "what times what equals 15" can be expressed algebraically as:
- x * y = 15
This simple equation introduces the concept of variables (x and y) representing unknown numbers. Solving this equation requires finding pairs of numbers (x and y) that satisfy the equation. As we've already established, the whole number solutions are (1, 15) and (3, 5), and their negative counterparts.
This algebraic representation opens up possibilities for exploring more complex equations where finding the factors becomes more challenging. For instance, consider the equation:
- x² - 16x + 45 = 0
This quadratic equation can be factored to (x-5)(x-9)=0, meaning the solutions are x=5 and x=9. This demonstrates the broader connection between factoring numbers and solving algebraic equations.
Applications of Factor Pairs: Real-World Examples
Understanding factors and factor pairs extends far beyond abstract mathematical concepts. They have practical applications in various real-world scenarios:
- Geometry: Calculating the area of a rectangle requires multiplying its length and width. If the area of a rectangle is 15 square units, its dimensions could be 1 unit by 15 units or 3 units by 5 units.
- Division: Knowing the factors of a number makes division easier. If you need to divide 15 items into equal groups, you can easily determine that you can divide them into groups of 1, 3, 5, or 15.
- Data Analysis: In statistics, factors are often used to analyze data sets and identify patterns. For example, if you're analyzing sales data and discover that the total sales for a particular product is 15 units, understanding the factors helps identify possible sales patterns.
- Coding and Programming: Factorization is a crucial concept in computer science, particularly in cryptography and algorithm optimization. Many algorithms rely on the efficient factorization of large numbers.
- Everyday Problem Solving: Even seemingly simple tasks like arranging objects in a grid or distributing resources equally often benefit from an understanding of factor pairs. For instance, if you have 15 candies and want to share them equally amongst friends, understanding the factors helps determine how many friends you can share with while ensuring everyone gets a whole number of candies.
Beyond Whole Numbers: Exploring Rational Numbers
While this article primarily focuses on whole number factors, it's worth mentioning that we can expand the search for numbers that multiply to 15 to include rational numbers (numbers that can be expressed as a fraction). For example, (1/2, 30), (1/3, 45), (2/3, 22.5), and infinitely many other pairs of numbers satisfy this condition. The possibilities become virtually limitless when we consider all rational numbers.
Frequently Asked Questions (FAQs)
Q: Are there any other numbers besides 1, 3, 5, and 15 that are factors of 15?
A: No, 1, 3, 5, and 15 are the only positive whole number factors of 15.
Q: What is the prime factorization of 15?
A: The prime factorization of 15 is 3 x 5.
Q: How can I find the factors of larger numbers?
A: There are several methods for finding factors of larger numbers, including using prime factorization, division, and factor trees. For very large numbers, specialized algorithms are used.
Q: What is the difference between a factor and a multiple?
A: A factor divides evenly into a number, while a multiple is the result of multiplying a number by another whole number. For example, 3 is a factor of 15, while 15 is a multiple of 3.
Conclusion: The Richness of a Simple Question
The seemingly simple question, "what times what equals 15?", unveils a surprisingly rich and complex mathematical landscape. From understanding fundamental concepts like factors and prime numbers to exploring algebraic equations and their applications in various fields, this question serves as a springboard for deeper mathematical exploration. The ability to identify factor pairs isn't just a basic arithmetic skill; it's a foundation for more advanced mathematical reasoning and problem-solving, with practical applications in many areas of life. This seemingly simple question encourages us to look beyond the immediate answer and appreciate the intricate connections within the world of mathematics.
Latest Posts
Latest Posts
-
Find Derivative Of An Integral
Sep 14, 2025
-
What Are The Factors 72
Sep 14, 2025
-
Different Types Of Scatter Graphs
Sep 14, 2025
-
Is 397 A Prime Number
Sep 14, 2025
-
What Is 0 05 In Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.