What Percentage Is 2 5
keralas
Sep 16, 2025 · 5 min read
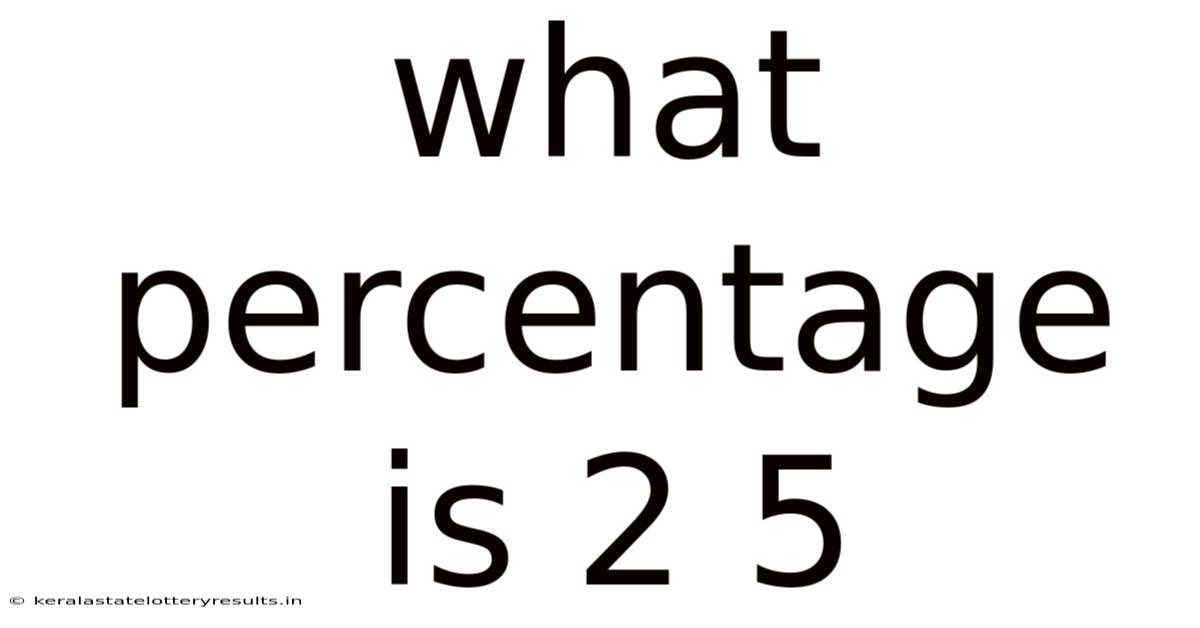
Table of Contents
What Percentage is 2/5? Understanding Fractions, Decimals, and Percentages
Understanding fractions, decimals, and percentages is a fundamental skill in mathematics with wide-reaching applications in everyday life, from calculating discounts and tips to comprehending data in various fields. This article comprehensively explains how to determine what percentage 2/5 represents, delving into the underlying principles and providing practical examples to solidify your understanding. We’ll cover the conversion process, explore related concepts, and address frequently asked questions to ensure a complete grasp of this essential mathematical concept.
Introduction: Fractions, Decimals, and Percentages – A Unified System
Before we dive into calculating the percentage equivalent of 2/5, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 2/5 means 2 parts out of a total of 5 parts.
-
Decimals: Represent a part of a whole using a base-ten system. The decimal point separates the whole number from the fractional part. For example, 0.4 represents four-tenths.
-
Percentages: Represent a part of a whole as a portion of 100. The percentage symbol (%) indicates that the number is a fraction of 100. For example, 40% means 40 out of 100.
These three systems are interconnected and readily convertible into one another. Mastering the conversions is crucial for effective mathematical problem-solving.
Converting 2/5 to a Decimal
The first step in determining what percentage 2/5 represents is converting the fraction into a decimal. To do this, we simply divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
Therefore, the decimal equivalent of 2/5 is 0.4.
Converting a Decimal to a Percentage
Now that we have the decimal equivalent (0.4), we can convert it to a percentage. To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.4 x 100 = 40
Therefore, 0.4 is equivalent to 40%.
Therefore, 2/5 is equal to 40%
To summarize the steps:
- Fraction to Decimal: 2 ÷ 5 = 0.4
- Decimal to Percentage: 0.4 x 100 = 40%
Understanding the Concept: Visual Representation
Visualizing the concept can enhance understanding. Imagine a pizza cut into 5 equal slices. If you eat 2 slices, you've consumed 2/5 of the pizza. This is equivalent to 0.4 of the pizza and represents 40% of the pizza.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world scenarios:
- Discounts: A 40% discount on a $100 item means you save $40 (40% of $100).
- Taxes: Sales tax is often expressed as a percentage. A 6% sales tax on a $50 item means you pay an additional $3 (6% of $50).
- Grades: Your grade in a class is often expressed as a percentage. A score of 85 out of 100 is an 85%.
- Statistics: Percentages are frequently used to represent data in charts and graphs. For instance, a survey may show that 40% of respondents prefer a particular brand.
- Financial Calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages.
Working with Larger Fractions and More Complex Percentages
The method outlined above can be applied to any fraction. For example, let's determine what percentage 3/8 is:
- Fraction to Decimal: 3 ÷ 8 = 0.375
- Decimal to Percentage: 0.375 x 100 = 37.5%
Therefore, 3/8 is equal to 37.5%.
For fractions that result in recurring decimals (like 1/3 = 0.333...), you can either express the percentage with a recurring decimal (33.333...%) or round it to a suitable number of decimal places (e.g., 33.3%).
Advanced Concepts: Percentage Increase and Decrease
Percentages are also used to describe increases and decreases. For instance:
-
Percentage Increase: If a quantity increases from 100 to 120, the percentage increase is calculated as follows:
(Increase / Original Value) x 100 = ((120 - 100) / 100) x 100 = 20%
-
Percentage Decrease: If a quantity decreases from 100 to 80, the percentage decrease is calculated as follows:
(Decrease / Original Value) x 100 = ((100 - 80) / 100) x 100 = 20%
Frequently Asked Questions (FAQ)
Q: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 40% to a fraction:
40% = 40/100 = 2/5
Q: What if I have a mixed number (like 1 2/5)? How do I convert it to a percentage?
A: First, convert the mixed number to an improper fraction: 1 2/5 = 7/5. Then follow the steps outlined above:
- Fraction to Decimal: 7 ÷ 5 = 1.4
- Decimal to Percentage: 1.4 x 100 = 140%
Q: Are there any shortcuts for converting fractions to percentages?
A: Some common fractions have easily memorized percentage equivalents (e.g., 1/2 = 50%, 1/4 = 25%, 1/5 = 20%). However, for most fractions, the division method is the most reliable.
Q: Why is understanding percentages important?
A: Understanding percentages is crucial for interpreting data, making financial decisions, comprehending discounts and sales, and navigating everyday situations involving proportions and ratios.
Conclusion: Mastering Percentage Calculations
Understanding how to convert fractions to percentages is a vital skill with numerous real-world applications. By grasping the fundamental principles and practicing the conversion methods, you can confidently tackle various mathematical problems and confidently navigate the world of percentages. Remember to break down the problem into smaller, manageable steps – from fraction to decimal, and then decimal to percentage – and always double-check your work to ensure accuracy. With practice and a solid understanding of the underlying concepts, you'll become proficient in working with fractions, decimals, and percentages. This proficiency will empower you to solve problems with greater ease and confidence in diverse academic and real-world settings.
Latest Posts
Latest Posts
-
What Is 45 Of 80
Sep 16, 2025
-
2 8 As A Decimal
Sep 16, 2025
-
How To Find A Frequency
Sep 16, 2025
-
200 000 Usd To Inr
Sep 16, 2025
-
Whats 20 Hours From Now
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.