What Is Half Of 3.5
keralas
Sep 18, 2025 · 5 min read
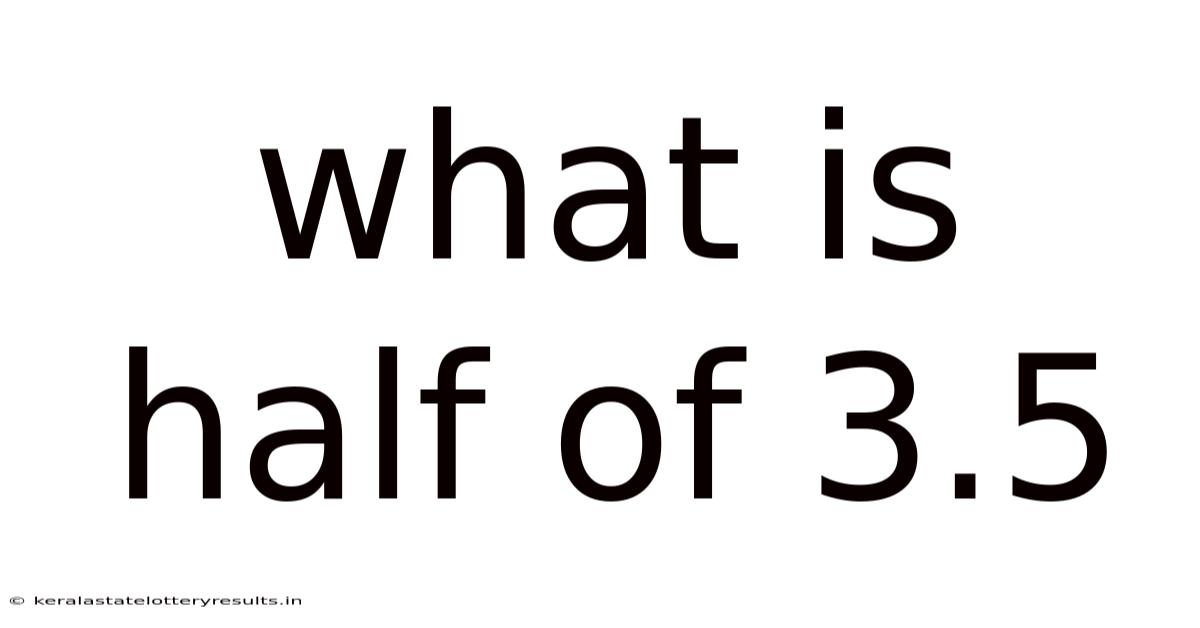
Table of Contents
What is Half of 3.5? A Deep Dive into Fractions, Decimals, and Problem-Solving
Finding half of a number is a fundamental concept in mathematics, crucial for everyday life and advanced calculations. This seemingly simple question, "What is half of 3.5?", opens the door to exploring various mathematical approaches, strengthening our understanding of fractions, decimals, and problem-solving strategies. This article will delve deep into this seemingly simple problem, providing a comprehensive understanding suitable for various learning levels.
Understanding the Concept of "Half"
Before jumping into the calculation, let's solidify our understanding of the term "half." Half simply means dividing something into two equal parts. Whether it's an apple, a pizza, or a number, finding half involves splitting it precisely in two. This basic concept is the foundation for understanding fractions and percentages.
Method 1: Fraction Approach
The most straightforward method to find half of 3.5 is using fractions. "Half" can be represented as the fraction 1/2. Therefore, finding half of 3.5 is equivalent to calculating (1/2) * 3.5.
To perform this calculation, we can either convert the decimal 3.5 into a fraction or find a common denominator. Let's convert 3.5 to a fraction: 3.5 can be written as 7/2 (since 3.5 = 3 + 1/2 = 6/2 + 1/2 = 7/2).
Now, the calculation becomes: (1/2) * (7/2) = 7/4
To express this as a decimal, we simply divide 7 by 4: 7 ÷ 4 = 1.75
Therefore, half of 3.5 is 1.75.
Method 2: Decimal Approach
Alternatively, we can directly work with decimals. Finding half of a number is the same as dividing it by 2. So, to find half of 3.5, we perform the division:
3.5 ÷ 2 = 1.75
This method provides a quicker solution, especially when dealing with simple decimal numbers. Again, we arrive at the answer: 1.75.
Method 3: Visual Representation
Visual aids can be particularly helpful for understanding fractions, especially for younger learners. Imagine a rectangle representing the number 3.5. Dividing this rectangle into two equal parts visually demonstrates that each part represents 1.75. This method reinforces the concept of "half" in a concrete, easily understandable way. This visual method is great for beginners to grasp the concept of division and fractions.
Expanding the Concept: Beyond 3.5
While we've solved the specific problem of finding half of 3.5, the methods employed can be generalized to find half of any number, whether it's a whole number, a decimal, or even a fraction. Let's explore some examples:
- Finding half of 7: 7 ÷ 2 = 3.5
- Finding half of 12.8: 12.8 ÷ 2 = 6.4
- Finding half of 2/3: (1/2) * (2/3) = 1/3
These examples illustrate the versatility of the fraction and decimal approaches. The key is to understand the fundamental principle of division by 2.
Understanding the Relationship Between Fractions and Decimals
This problem also serves as an excellent opportunity to reinforce the relationship between fractions and decimals. We've demonstrated how to convert a decimal (3.5) into a fraction (7/2) and vice-versa, converting a fraction (7/4) into a decimal (1.75). This interconversion is a critical skill in mathematics, facilitating calculations and problem-solving across different number systems. Mastering this conversion allows for flexibility in choosing the most efficient method for a particular problem.
Practical Applications: Real-World Examples
The ability to find half of a number has numerous practical applications in everyday life:
- Sharing: Dividing snacks, chores, or resources equally among two people.
- Cooking: Halving recipes to accommodate smaller portions.
- Shopping: Calculating discounts or comparing prices.
- Measurement: Converting units or calculating distances.
- Finance: Determining half of a payment, or splitting a bill.
Understanding this seemingly simple mathematical concept makes many everyday tasks much easier and more efficient. It underpins much more complex mathematical concepts and applications.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to find half of 3.5?
A: Absolutely! Calculators provide a quick and efficient way to solve this type of problem. Simply enter 3.5 ÷ 2 and the calculator will display the answer, 1.75.
Q: Is there any other way to represent half of 3.5?
A: Yes, besides 1.75, you can represent it as 7/4 (as a fraction) or as 175/100 (as another fraction). All represent the same value.
Q: What if I need to find a third or a quarter of 3.5?
A: To find a third, you divide 3.5 by 3 (3.5 ÷ 3 ≈ 1.1667). To find a quarter, you divide 3.5 by 4 (3.5 ÷ 4 = 0.875). The approach remains the same; divide the number by the desired denominator of the fraction.
Q: Why is understanding "half" important in higher-level mathematics?
A: The concept of halving forms the basis for numerous mathematical concepts, including proportions, ratios, percentages, and more advanced topics in algebra, calculus, and beyond. It is a building block for more sophisticated mathematical understanding.
Conclusion
Finding half of 3.5, while seemingly a trivial problem, offers a valuable opportunity to explore fundamental mathematical concepts, including fractions, decimals, and problem-solving strategies. The ability to solve this problem efficiently and accurately is a testament to a strong understanding of basic arithmetic and its applications. Mastering these basic mathematical operations forms a solid foundation for tackling more complex challenges in the future. Remember, even seemingly simple concepts, when explored thoroughly, reveal a wealth of underlying principles and practical applications. The more we understand the 'why' behind the 'how', the stronger our mathematical foundation becomes.
Latest Posts
Latest Posts
-
How To Minus Mixed Numbers
Sep 18, 2025
-
What Is Half Of 18
Sep 18, 2025
-
Prisma Treat Decimal As Number
Sep 18, 2025
-
What Is 75 Degrees C
Sep 18, 2025
-
Square Root Of 147 Simplified
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.