What Is 70 Of 25
keralas
Sep 13, 2025 · 5 min read
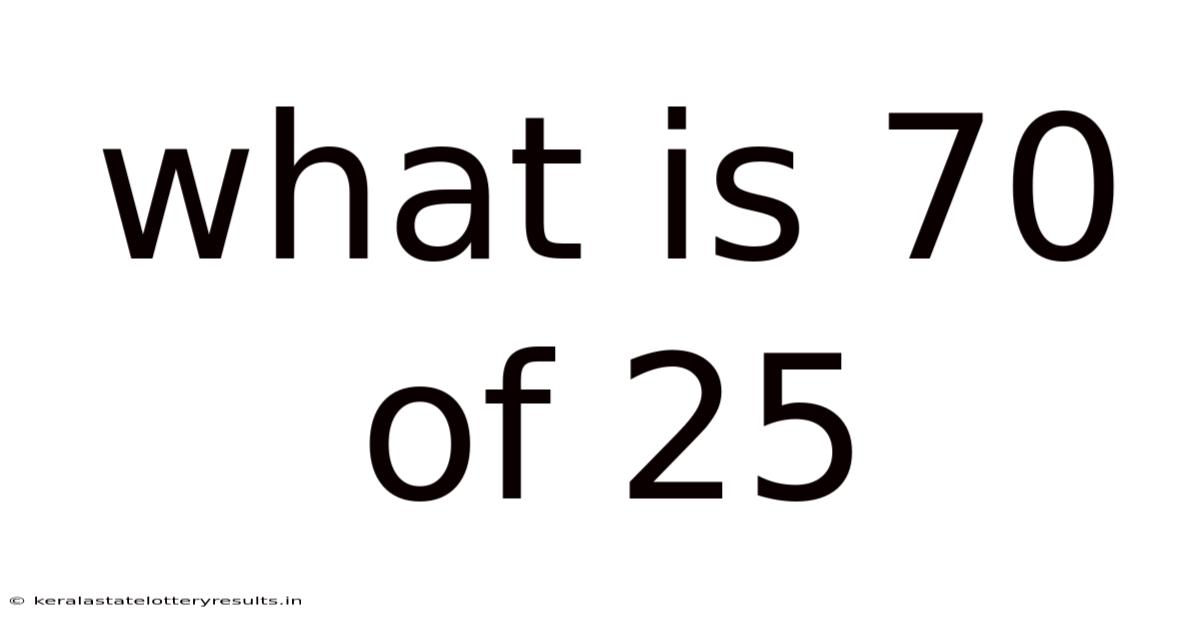
Table of Contents
What is 70% of 25? Understanding Percentages and Their Applications
Finding 70% of 25 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for numerous applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only show you how to calculate 70% of 25 but also delve deeper into the concept of percentages, exploring various methods of calculation and highlighting its importance across different fields.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" ("per cent" from Latin). Therefore, 70% means 70 out of 100, which can be written as the fraction 70/100 or the decimal 0.70. Understanding this fundamental concept is key to solving percentage problems.
Method 1: Using Decimal Conversion
This is perhaps the most straightforward method. To find 70% of 25, we first convert the percentage to a decimal. As mentioned above, 70% is equal to 0.70. Then, we simply multiply this decimal by the number we're interested in, which is 25:
0.70 x 25 = 17.5
Therefore, 70% of 25 is 17.5.
Method 2: Using Fraction Conversion
Another way to solve this problem involves converting the percentage to a fraction. 70% can be written as 70/100. We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 10:
70/100 = 7/10
Now, we multiply this fraction by 25:
(7/10) x 25 = 175/10 = 17.5
Again, we arrive at the answer: 70% of 25 is 17.5.
Method 3: Proportion Method
This method uses the concept of proportion. We set up a proportion where x represents the unknown value (70% of 25):
70/100 = x/25
To solve for x, we cross-multiply:
70 x 25 = 100x
1750 = 100x
x = 1750/100
x = 17.5
Once more, we find that 70% of 25 is 17.5.
Why is Understanding Percentages Important?
The ability to calculate percentages is a fundamental skill with wide-ranging applications across numerous disciplines. Here are just a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on understanding percentages. Whether you're trying to figure out the total cost of an item after tax, comparing loan interest rates, or tracking your investment portfolio's performance, percentage calculations are essential.
-
Retail and Sales: Retailers use percentages to calculate discounts, markups, and sales tax. Understanding these calculations is crucial for both businesses and consumers. For instance, calculating the final price of an item after a 20% discount requires a solid grasp of percentages. Similarly, analyzing sales figures and comparing year-over-year growth often involves percentage change calculations.
-
Science and Statistics: Percentages are used extensively in scientific research and statistical analysis to represent data, probabilities, and proportions. For example, expressing experimental results, analyzing survey data, or calculating the probability of an event often involves percentage calculations.
-
Everyday Life: Even in everyday life, understanding percentages is useful for tasks such as calculating tips in restaurants, understanding nutritional information on food labels, or figuring out the percentage of completion on a project.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond simple percentage calculations like finding 70% of 25, understanding percentage increase and decrease is also crucial.
-
Percentage Increase: This involves calculating the increase in a value as a percentage of the original value. For example, if a price increases from $20 to $25, the percentage increase is calculated as follows:
Increase = $25 - $20 = $5
Percentage Increase = (Increase / Original Value) x 100% = ($5 / $20) x 100% = 25%
-
Percentage Decrease: This is the inverse of percentage increase, calculating the decrease in a value as a percentage of the original value. For example, if a price decreases from $25 to $20, the percentage decrease is:
Decrease = $25 - $20 = $5
Percentage Decrease = (Decrease / Original Value) x 100% = ($5 / $25) x 100% = 20%
Solving More Complex Percentage Problems
Let's consider a more complex example. Suppose a store offers a 30% discount on an item initially priced at $80. Then, a 5% sales tax is added to the discounted price. What is the final price?
-
Calculate the discount: 30% of $80 = 0.30 x $80 = $24
-
Calculate the discounted price: $80 - $24 = $56
-
Calculate the sales tax: 5% of $56 = 0.05 x $56 = $2.80
-
Calculate the final price: $56 + $2.80 = $58.80
The final price of the item after the discount and sales tax is $58.80. This example demonstrates how multiple percentage calculations can be combined to solve real-world problems.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on the specific problem. However, converting the percentage to a decimal and multiplying is generally a quick and efficient approach for most situations.
Q: How can I calculate percentages without a calculator?
A: For simpler percentages (like 10%, 25%, 50%), you can use mental math techniques. For example, 10% is simply dividing by 10, and 50% is dividing by 2. For more complex percentages, you can use the fraction method or the proportion method, though these might require more manual calculations.
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include incorrectly converting percentages to decimals, forgetting to account for sales tax or other additional fees, and misinterpreting the base value upon which the percentage is calculated. Carefully reading the problem and breaking it down into smaller steps can help prevent these errors.
Q: Are there any online tools or calculators available for percentage calculations?
A: Yes, many free online percentage calculators are readily available. These can be helpful for double-checking your work or for more complex percentage problems.
Conclusion
Calculating 70% of 25, as we've seen, yields 17.5. However, this simple calculation serves as a gateway to a broader understanding of percentages and their immense practical importance. From managing personal finances to analyzing complex scientific data, the ability to confidently work with percentages is a valuable skill that enhances problem-solving capabilities across numerous disciplines. Mastering percentage calculations empowers you to navigate the numerical world with greater ease and confidence. Remember to practice regularly, explore different calculation methods, and always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
How Do You Spell 3
Sep 13, 2025
-
Convert 35 Cm To Inches
Sep 13, 2025
-
Is 12 A Composite Number
Sep 13, 2025
-
110 Degrees Celsius To Fahrenheit
Sep 13, 2025
-
What Decimal Is 5 8
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.