What Is 60 Of 90
keralas
Sep 16, 2025 · 5 min read
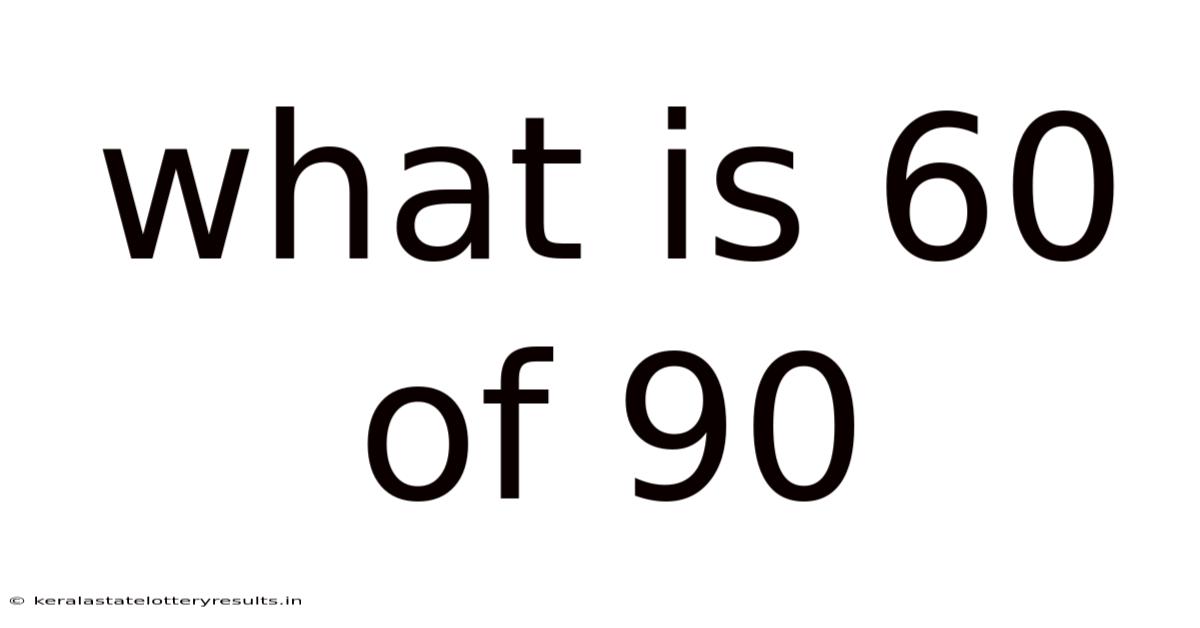
Table of Contents
What is 60 of 90? Understanding Fractions, Percentages, and Ratios
This article delves into the seemingly simple question: "What is 60 of 90?" While the immediate answer might seem obvious to some, we'll unpack this problem to explore the underlying mathematical concepts, highlighting different approaches to solve it and extending the understanding to broader applications of fractions, percentages, and ratios. This will equip you with the skills to tackle similar problems with confidence and a deeper understanding of fundamental mathematical principles.
Introduction: Deconstructing the Problem
The question "What is 60 of 90?" is essentially asking us to find the relationship between 60 and 90. This relationship can be expressed in several ways: as a fraction, a percentage, or a ratio. Each representation provides a different perspective on the same underlying mathematical concept. Understanding these different representations is key to tackling more complex problems.
Method 1: Using Fractions
The most straightforward approach is to represent the relationship as a fraction. "60 of 90" can be written as the fraction 60/90. This fraction represents the part (60) compared to the whole (90).
To simplify this fraction, we find the greatest common divisor (GCD) of 60 and 90, which is 30. Dividing both the numerator and the denominator by 30, we get:
60/90 = (60 ÷ 30) / (90 ÷ 30) = 2/3
Therefore, 60 is two-thirds (2/3) of 90. This is a simplified and concise representation of the relationship.
Method 2: Using Percentages
Percentages provide another way to express the relationship between 60 and 90. A percentage represents a fraction out of 100. To convert the fraction 60/90 to a percentage, we perform the following calculation:
(60/90) * 100% = (2/3) * 100% ≈ 66.67%
Therefore, 60 is approximately 66.67% of 90. This representation is particularly useful for comparisons and for expressing proportions in everyday contexts. The slight rounding is necessary because 2/3 is a recurring decimal.
Method 3: Using Ratios
Ratios express the relationship between two or more quantities. The ratio of 60 to 90 can be written as 60:90. Similar to fractions, this ratio can be simplified by dividing both numbers by their GCD (30):
60:90 = 2:3
This simplified ratio indicates that for every 2 units of one quantity, there are 3 units of the other. Ratios are frequently used in various fields, including scaling recipes, comparing sizes, and analyzing data proportions.
Expanding the Understanding: Proportions and Problem Solving
The concept of "60 of 90" extends beyond a simple calculation. Understanding the relationship between these numbers allows us to solve more complex proportional problems. For instance:
-
Scaling: If a recipe calls for 90 grams of flour and you only want to make two-thirds of the recipe, how much flour do you need? Knowing that 60 is 2/3 of 90, you would use 60 grams of flour.
-
Percentage increase/decrease: If a value increases from 60 to 90, what is the percentage increase? The increase is 30, and the percentage increase is calculated as (30/60) * 100% = 50%. Conversely, if a value decreases from 90 to 60, the percentage decrease is (30/90) * 100% = 33.33%.
-
Real-world applications: This concept applies to many real-world scenarios, such as calculating discounts, determining the proportion of a population, or analyzing survey results. For example, if 60 out of 90 students passed an exam, the pass rate is 66.67%.
Further Exploration: Decimals and Recurring Decimals
The fraction 2/3, representing the simplified form of 60/90, is a recurring decimal. This means that its decimal representation (0.66666...) continues infinitely without repeating in a finite pattern. Understanding recurring decimals is crucial in many mathematical and scientific applications.
Beyond the Basics: Advanced Concepts
The simple problem of finding "60 of 90" opens doors to more sophisticated mathematical ideas:
-
Algebra: We can express the relationship algebraically. Let x represent "60 of 90." Then, we can write the equation: x/90 = 60/90. Solving for x gives x = 60. This simple example shows how algebraic representation can handle more complex proportional problems.
-
Calculus: In calculus, the concept of limits and infinitesimals provides a way to handle infinitely small changes and relationships, which are vital for understanding concepts such as derivatives and integrals. While seemingly unrelated to this basic problem, the principles of ratios and proportions are foundational to calculus.
Frequently Asked Questions (FAQ)
-
What is the simplest form of the fraction 60/90? The simplest form is 2/3.
-
How do I convert a fraction to a percentage? Multiply the fraction by 100%.
-
What is the ratio of 60 to 90? The ratio is 2:3.
-
Can I use a calculator to solve this problem? Yes, a calculator can be used to perform the division (60/90) and the multiplication ((60/90)*100) to obtain the decimal and percentage answers respectively.
-
What if the numbers were larger or smaller? The same principles apply. Simplify the fraction by finding the GCD and then convert to a percentage or express as a ratio as needed.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 60 of 90?", provides a springboard for exploring fundamental mathematical concepts – fractions, percentages, ratios, and their applications in various contexts. Understanding these concepts is crucial not just for academic success but also for navigating everyday life and tackling more complex quantitative challenges. By mastering these fundamental building blocks, you equip yourself with essential tools for problem-solving and a deeper appreciation for the power and elegance of mathematics. Remember that practice is key! Try working through similar problems using different methods to solidify your understanding. The more you practice, the more comfortable you'll become with these important mathematical skills.
Latest Posts
Latest Posts
-
Quadrilateral With 4 Equal Sides
Sep 16, 2025
-
3 4 In A Number Line
Sep 16, 2025
-
One Fifth In Decimal Form
Sep 16, 2025
-
Sum Of First 100 Numbers
Sep 16, 2025
-
2 7 8 As Decimal
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.