What Is 50 Of 25
keralas
Sep 14, 2025 · 5 min read
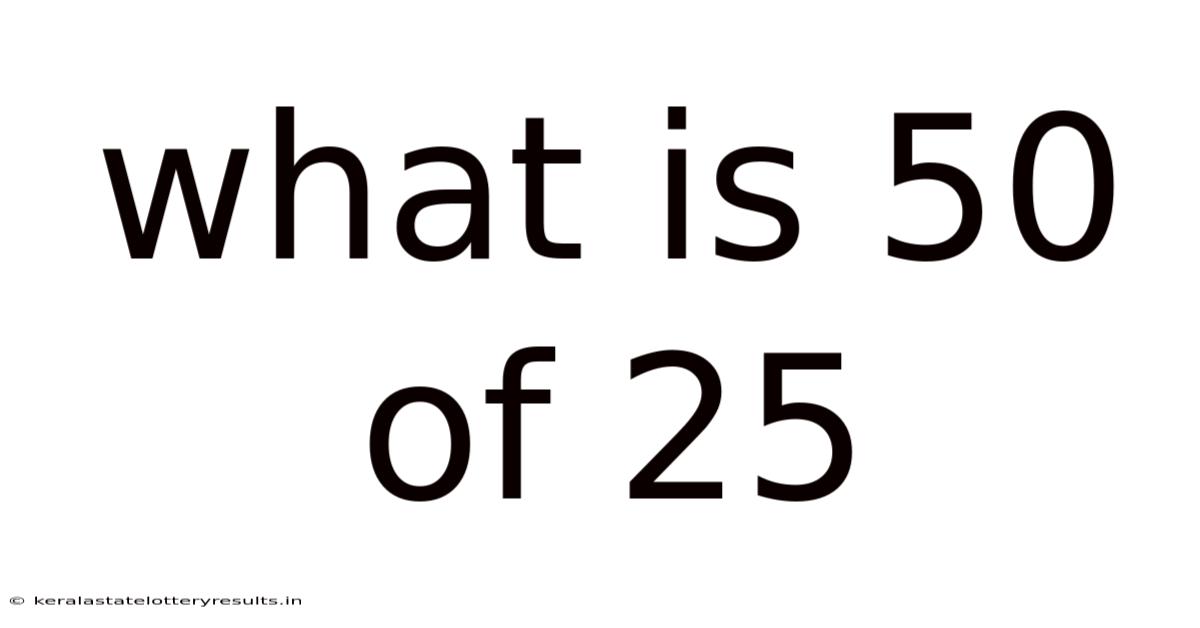
Table of Contents
What is 50% of 25? A Deep Dive into Percentages and Their Applications
Finding 50% of 25 might seem like a simple arithmetic problem, solvable in a flash. However, understanding the underlying principles of percentages opens up a world of practical applications, from calculating discounts in a shop to understanding complex financial models. This article will not only answer the question "What is 50% of 25?" but also delve into the concept of percentages, exploring different methods of calculation, and showcasing real-world examples to solidify your understanding. By the end, you’ll be confident in tackling percentage problems of any complexity.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." The symbol "%" is used to represent percentages. So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Understanding this fundamental concept is crucial. Percentages provide a standardized way to compare different proportions. Whether we're talking about exam scores (85%), sales tax (6%), or inflation rates (2%), percentages allow us to easily grasp the relative size or magnitude of these quantities.
Method 1: The Fraction Method
One of the easiest ways to calculate a percentage of a number is to convert the percentage into a fraction and then multiply.
To find 50% of 25, we first convert 50% to a fraction:
50% = 50/100 = 1/2
Now, we multiply this fraction by 25:
(1/2) * 25 = 25/2 = 12.5
Therefore, 50% of 25 is 12.5.
Method 2: The Decimal Method
Another common approach involves converting the percentage into a decimal and then multiplying.
To convert 50% to a decimal, we divide it by 100:
50% / 100 = 0.5
Now, we multiply this decimal by 25:
0.5 * 25 = 12.5
Again, we find that 50% of 25 is 12.5.
Method 3: Using Proportions
The concept of proportion offers a more visual and intuitive approach to solving percentage problems. We can set up a proportion to find the unknown value (x) which represents 50% of 25.
The proportion looks like this:
50/100 = x/25
To solve for x, we cross-multiply:
50 * 25 = 100 * x
1250 = 100x
x = 1250 / 100
x = 12.5
This method confirms that 50% of 25 is 12.5.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in various aspects of daily life and professional fields:
-
Shopping: Calculating discounts, sales tax, and tips. For instance, a 20% discount on a $50 item can be calculated using the methods described above.
-
Finance: Determining interest rates on loans and investments, calculating returns on investments (ROI), and analyzing financial statements. Understanding percentage changes in stock prices or interest rates is crucial for making informed financial decisions.
-
Science: Expressing experimental results, representing data in graphs and charts, and analyzing statistical data. Percentage changes in scientific measurements are often used to show the significance of experimental findings.
-
Health: Understanding body fat percentages, calculating medication dosages, and interpreting health statistics. Doctors and other healthcare professionals rely on percentage calculations for diagnosis and treatment.
-
Education: Calculating grades, assessing student performance, and understanding test scores. Understanding your percentage score on an exam provides a clear indication of your performance.
Beyond 50% of 25: Tackling More Complex Percentage Problems
While the example of 50% of 25 is relatively straightforward, the principles can be applied to more complex scenarios. Let's explore some examples:
Example 1: Finding a percentage of a larger number:
What is 15% of 300?
Using the decimal method:
15% = 0.15
0.15 * 300 = 45
Therefore, 15% of 300 is 45.
Example 2: Finding the percentage one number represents of another:
What percentage of 80 is 20?
We can set up a proportion:
x/100 = 20/80
Cross-multiplying:
80x = 2000
x = 2000/80
x = 25
Therefore, 20 is 25% of 80.
Example 3: Calculating percentage increase or decrease:
A product initially cost $100 and its price increased to $120. What is the percentage increase?
Percentage increase = [(New value - Old value) / Old value] * 100
Percentage increase = [(120 - 100) / 100] * 100 = 20%
Frequently Asked Questions (FAQ)
Q1: What are some common mistakes people make when calculating percentages?
- Confusing percentage with decimal: Forgetting to divide the percentage by 100 before multiplying.
- Incorrect order of operations: Multiplying before converting to a decimal or fraction.
- Rounding errors: Not carrying enough decimal places during calculations, leading to inaccuracies.
Q2: Are there any online calculators or tools available to help with percentage calculations?
Yes, many online calculators are readily available to perform percentage calculations. These tools can be helpful for checking your work or for complex calculations.
Q3: How can I improve my understanding and skills in percentage calculations?
- Practice regularly: Solve various percentage problems to build your confidence and proficiency.
- Use different methods: Try solving the same problem using multiple methods to strengthen your understanding of the underlying concepts.
- Seek help when needed: Don't hesitate to consult textbooks, online resources, or tutors if you're struggling with a particular concept.
Conclusion
Finding 50% of 25, while seemingly simple, serves as a gateway to understanding the broader world of percentage calculations. Mastering these calculations is crucial for success in various aspects of life, from everyday budgeting to complex financial analysis. By understanding the different methods, applying them to real-world scenarios, and addressing common errors, you can confidently tackle percentage problems of any complexity and unlock a deeper understanding of this fundamental mathematical concept. Remember to practice regularly and utilize different methods to solidify your grasp on this important skill. The ability to calculate percentages fluently will empower you to make informed decisions and navigate the numerical world with greater ease and confidence.
Latest Posts
Latest Posts
-
Derivative Of 2 Over X
Sep 14, 2025
-
Is 509 A Prime Number
Sep 14, 2025
-
Square Root Of 34 Simplified
Sep 14, 2025
-
1 3 In Fraction Form
Sep 14, 2025
-
3 To The 9th Power
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.