What Is 25 Of 16
keralas
Sep 13, 2025 · 5 min read
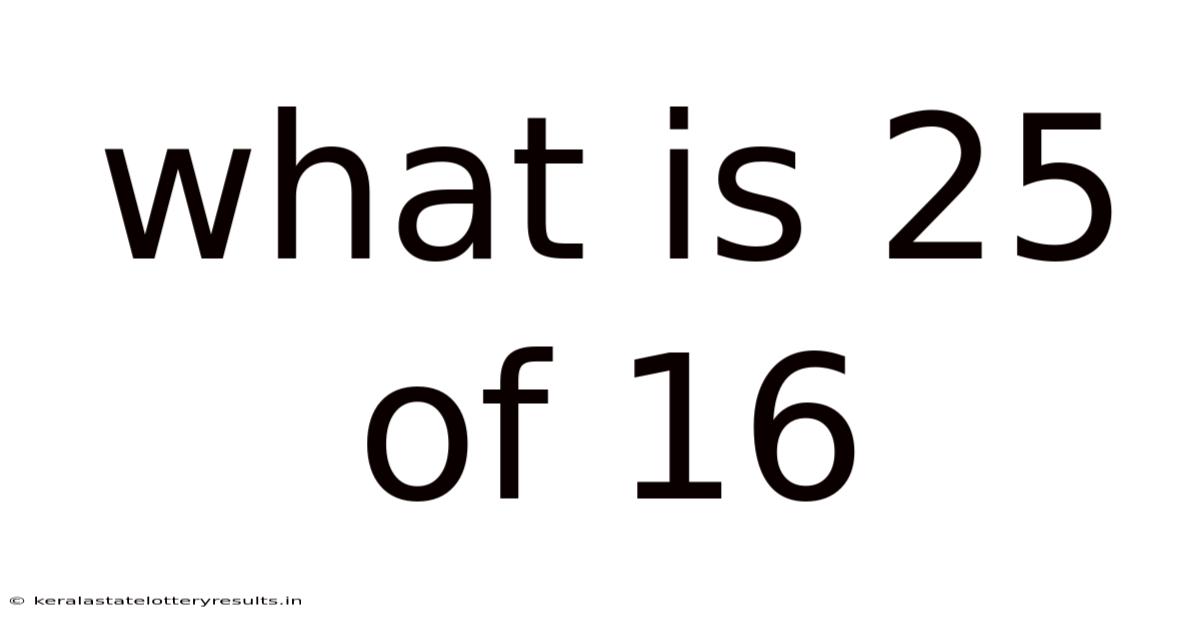
Table of Contents
What is 25% of 16? A Comprehensive Guide to Percentages and their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending statistics and financial reports. This article will delve into the question "What is 25% of 16?" not just by providing the answer, but by explaining the underlying concepts and methods involved in percentage calculations. We'll explore various approaches, ensuring a thorough understanding for learners of all levels. This will also cover practical examples and frequently asked questions, making this a comprehensive guide to percentages.
Understanding Percentages
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "per hundred." The symbol "%" is used to denote percentages. For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Method 1: Converting Percentage to Decimal
The most straightforward method to calculate 25% of 16 is to convert the percentage to its decimal equivalent and then multiply it by the number.
-
Convert the percentage to a decimal: 25% is equivalent to 25/100 = 0.25.
-
Multiply the decimal by the number: 0.25 * 16 = 4
Therefore, 25% of 16 is $\boxed{4}$.
Method 2: Using Fractions
Alternatively, we can solve this using fractions.
-
Convert the percentage to a fraction: 25% can be written as the fraction 25/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 25. This simplifies to 1/4.
-
Multiply the fraction by the number: (1/4) * 16 = 16/4 = 4
Again, we find that 25% of 16 is $\boxed{4}$.
Method 3: Proportion Method
The proportion method offers a more visual approach to understanding percentage calculations. We set up a proportion:
- Part/Whole = Percentage/100
In this case:
- x/16 = 25/100
To solve for x (which represents 25% of 16), we cross-multiply:
- 100x = 25 * 16
- 100x = 400
- x = 400/100
- x = 4
Thus, 25% of 16 is $\boxed{4}$.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
-
Sales and Discounts: Stores frequently advertise sales with percentages. For example, a 25% discount on a $16 item means you save 25% of $16, which is $4, and you pay $12.
-
Taxes: Calculating sales tax involves finding a percentage of the original price. If the sales tax is 6%, and an item costs $16, the tax amount is 6% of $16, which is $0.96.
-
Tips: Calculating tips in restaurants usually involves finding a percentage of the bill. A 15% tip on a $16 meal would be $2.40.
-
Interest Rates: Understanding interest rates on loans and savings accounts relies heavily on percentage calculations. If you have a savings account with a 3% annual interest rate and $16 in your account, you will earn $0.48 in interest after one year.
-
Statistics and Data Analysis: Percentages are frequently used to represent data in charts and graphs, making it easier to visualize and interpret information.
Expanding on Percentage Concepts: Beyond the Basics
While calculating 25% of 16 is a simple example, mastering percentages involves understanding various related concepts:
-
Calculating the Percentage Increase or Decrease: This involves finding the difference between two values and expressing it as a percentage of the original value. For example, if a value increases from 10 to 16, the percentage increase is [(16-10)/10] * 100% = 60%.
-
Finding the Original Value: Sometimes, you know the percentage and the resulting value, and need to find the original value. For example, if 25% of a number is 4, the original number can be found by solving the equation 0.25x = 4, which gives x = 16.
-
Working with Compound Percentages: Compound percentages involve applying a percentage multiple times. This is common in finance, where interest is often compounded annually or monthly.
-
Understanding Percentage Points: It's important to distinguish between percentage points and percentages. A change from 25% to 30% is a 5 percentage point increase, but a 20% increase (5/25 * 100%).
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a different percentage of 16?
A: You can follow the same methods described above, substituting the desired percentage for 25%. For example, to calculate 10% of 16, you would convert 10% to 0.10 and multiply it by 16 (0.10 * 16 = 1.6).
Q: Can I use a calculator to calculate percentages?
A: Yes, most calculators have a percentage function. Simply enter the number, press the percentage button, and then multiply by the percentage you are interested in.
Q: Why is understanding percentages important?
A: Understanding percentages is essential for everyday life, from managing finances to interpreting data and making informed decisions. It’s a crucial skill in various fields, including business, finance, science, and engineering.
Q: Are there any online resources to practice percentage calculations?
A: Yes, numerous online resources, including educational websites and apps, offer practice exercises and tutorials on percentage calculations.
Q: What if the percentage involves decimals, such as 25.5% of 16?
A: The methods remain the same. Convert 25.5% to 0.255 and multiply it by 16 (0.255 * 16 = 4.08).
Q: How can I improve my understanding of percentages?
A: Consistent practice is key. Work through various examples, use different methods to solve the same problem, and try to apply percentages to real-life scenarios.
Conclusion
This comprehensive guide demonstrates that calculating 25% of 16 is a straightforward process, achievable through several methods. The answer is unequivocally 4. However, the true value of this exercise lies not just in finding the answer, but in understanding the fundamental concepts of percentages and their diverse applications. By mastering percentage calculations, you equip yourself with a crucial skill that will serve you well in numerous aspects of life and various academic or professional pursuits. Remember that consistent practice and exploring various problem-solving approaches are key to solidifying your understanding of this vital mathematical concept.
Latest Posts
Latest Posts
-
What Is 10 Of 50000
Sep 13, 2025
-
Lcm Of 3 4 5
Sep 13, 2025
-
How To Find Common Ratio
Sep 13, 2025
-
Sum Or Difference Of Cubes
Sep 13, 2025
-
30 Percent As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.