What Is 2/3 Plus 2/3
keralas
Sep 15, 2025 · 5 min read
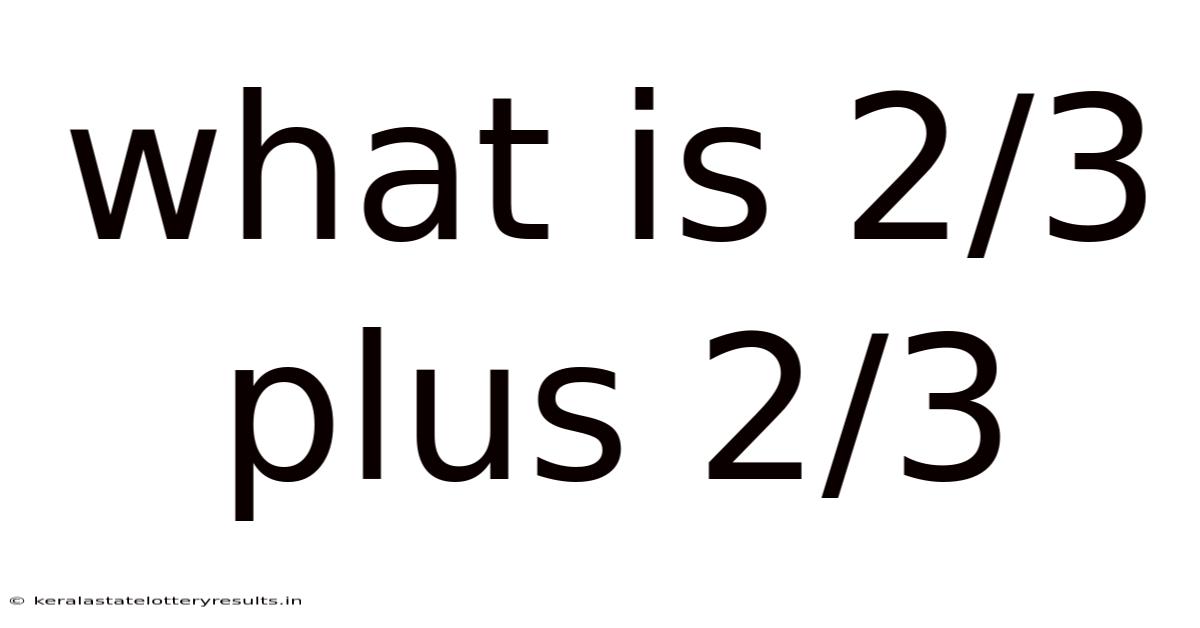
Table of Contents
What is 2/3 Plus 2/3? A Deep Dive into Fraction Addition
This article explores the seemingly simple question: "What is 2/3 plus 2/3?" While the answer might seem obvious to some, delving deeper reveals fundamental concepts in arithmetic, particularly regarding fractions. We'll cover the basic calculation, explore the underlying principles, and even touch upon real-world applications, ensuring a comprehensive understanding for learners of all levels. This exploration will also cover various methods for solving this type of problem and explain why understanding fractions is crucial for various mathematical concepts.
Understanding Fractions: The Building Blocks
Before we tackle the addition problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 2/3, the numerator is 2, and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Visualizing fractions is often helpful. Imagine a pizza cut into 3 equal slices. The fraction 2/3 represents having 2 of those 3 slices. Understanding this visual representation makes the concept of fractions more intuitive and less abstract.
Adding Fractions: A Step-by-Step Guide
Adding fractions requires a crucial understanding: you can only add fractions with the same denominator. If the denominators are different, you need to find a common denominator before adding. Fortunately, in our problem (2/3 + 2/3), the denominators are already the same.
Step 1: Check the Denominators
In the equation 2/3 + 2/3, both fractions have a denominator of 3. This simplifies the process significantly.
Step 2: Add the Numerators
Since the denominators are the same, we simply add the numerators: 2 + 2 = 4.
Step 3: Keep the Denominator
The denominator remains unchanged. It stays as 3.
Step 4: Simplify the Result (If Necessary)
This gives us the result 4/3. This is an improper fraction, meaning the numerator is larger than the denominator. We can convert this into a mixed number which combines a whole number and a fraction. To do this, we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1.
This means 4/3 is equivalent to 1 and 1/3.
Therefore, 2/3 + 2/3 = 4/3 = 1 1/3
Visual Representation of the Addition
Imagine two pizzas, each cut into three equal slices. If you take two slices from the first pizza (2/3) and two slices from the second pizza (2/3), you will have a total of four slices. Since each pizza had three slices, you have four slices out of a possible six slices (considering both pizzas). This simplifies to 2/3 if you combine the two pizzas into a single entity but that simplifies to 4/3.
Beyond the Basics: Different Denominators
Let's consider a slightly more complex scenario, adding fractions with different denominators. For example, what is 1/2 + 1/4?
Step 1: Find the Least Common Denominator (LCD)
The LCD is the smallest number that is a multiple of both denominators. In this case, the LCD of 2 and 4 is 4.
Step 2: Convert Fractions to Equivalent Fractions with the LCD
We need to convert 1/2 to an equivalent fraction with a denominator of 4. To do this, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4.
Step 3: Add the Numerators
Now we have 2/4 + 1/4. We add the numerators: 2 + 1 = 3.
Step 4: Keep the Denominator
The denominator remains 4.
Step 5: Simplify (If Necessary)
The result is 3/4, which is already in its simplest form. Therefore, 1/2 + 1/4 = 3/4
Real-World Applications of Fraction Addition
Understanding fraction addition isn't just an academic exercise; it has numerous practical applications in everyday life. Consider these examples:
- Cooking and Baking: Recipes often require fractional measurements of ingredients. Adding fractions is crucial for accurate measurements. For example, if a recipe calls for 1/2 cup of sugar and 1/4 cup of butter, you need to be able to add these fractions to understand the total amount of liquid ingredients.
- Measuring and Construction: Carpenters, builders, and other tradespeople frequently use fractions when measuring and cutting materials. Accurate measurements are essential, and adding fractions ensures precision.
- Finance: Understanding fractions is important when dealing with percentages, which are essentially fractions with a denominator of 100. Calculating discounts, interest rates, and other financial aspects often involves adding fractions.
- Data Analysis: In various fields, interpreting data often involves working with fractions and percentages. Adding fractions becomes essential to summarizing and comparing data points.
Frequently Asked Questions (FAQ)
Q: What happens if the numerator is greater than the denominator after adding fractions?
A: This results in an improper fraction. You should convert it into a mixed number for a clearer representation.
Q: Can I add fractions with different denominators directly?
A: No, you must first find the least common denominator and convert the fractions to equivalent fractions with that denominator before adding.
Q: What if the fractions are negative?
A: The same principles apply. Remember the rules of adding and subtracting negative numbers. For example, -2/3 + (-2/3) = -4/3
Q: Is there a shortcut for adding fractions with the same denominator?
A: Yes, simply add the numerators and keep the denominator.
Conclusion: Mastering Fractions – A Foundation for Success
Mastering fraction addition is fundamental to success in mathematics and beyond. It's a building block for more complex mathematical concepts, and its practical applications extend to various aspects of daily life. While the initial concept might seem daunting, by breaking down the process into manageable steps and understanding the underlying principles, anyone can confidently add fractions and apply this skill to solve real-world problems. Remember to visualize the fractions, practice regularly, and don't hesitate to revisit the fundamental concepts whenever needed. The seemingly simple question "What is 2/3 plus 2/3?" opens the door to a deeper understanding of a crucial mathematical concept. And the answer, as we have thoroughly explored, is 4/3 or 1 1/3.
Latest Posts
Latest Posts
-
What Is 1 3 Of 50
Sep 15, 2025
-
Is 15 Prime Or Composite
Sep 15, 2025
-
12 Is A Multiple Of
Sep 15, 2025
-
How Do Negative Powers Work
Sep 15, 2025
-
10 To Power Of 100
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Plus 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.