What Is 15 Of 25
keralas
Sep 16, 2025 · 5 min read
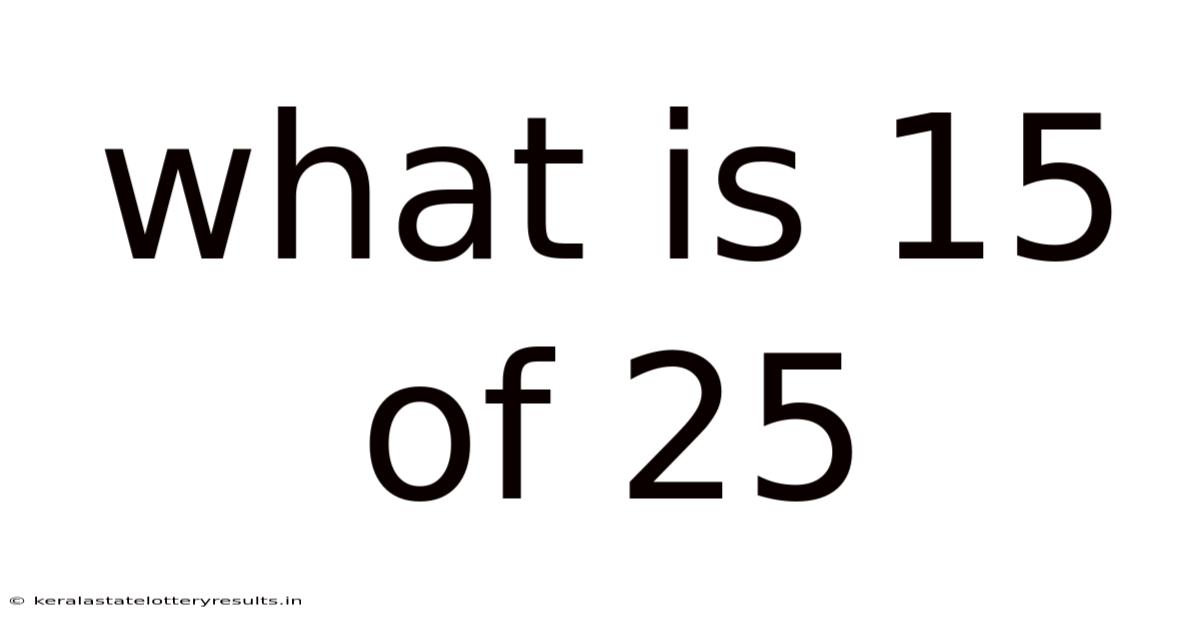
Table of Contents
What is 15 of 25? Unpacking Percentages and Fractions
This article delves into the seemingly simple question: "What is 15 of 25?" While the answer might seem immediately obvious to some, understanding the underlying concepts of fractions, percentages, and ratios is crucial for a broader grasp of mathematics. We'll explore multiple ways to solve this problem, highlighting the different mathematical principles involved and expanding our understanding beyond a single numerical answer. This will equip you with the skills to tackle similar problems and to confidently interpret fractional and percentage relationships in various contexts.
Understanding the Problem: Fractions and Ratios
The question "What is 15 of 25?" essentially asks us to determine the fraction 15/25 and its equivalent representations. This involves understanding the concept of a ratio: a comparison of two quantities. In this case, the ratio is 15 to 25, meaning we are comparing the part (15) to the whole (25). The fraction 15/25 represents this ratio.
To find the answer, we need to simplify this fraction and explore its equivalent expressions as a decimal and a percentage. This exploration will reinforce the interconnectedness of these different mathematical representations.
Method 1: Simplifying the Fraction
The simplest approach to answering "What is 15 of 25?" is to simplify the fraction 15/25. This involves finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (25). The GCD is the largest number that divides both 15 and 25 without leaving a remainder.
In this case, the GCD of 15 and 25 is 5. Dividing both the numerator and the denominator by 5, we get:
15 ÷ 5 = 3 25 ÷ 5 = 5
Therefore, the simplified fraction is 3/5. This means that 15 is 3/5 of 25.
Method 2: Converting to a Decimal
Converting the fraction 3/5 to a decimal involves dividing the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
So, 15 is 0.6 of 25. This decimal representation provides a different perspective on the relationship between 15 and 25.
Method 3: Calculating the Percentage
To express 15 as a percentage of 25, we can use the following formula:
(Part / Whole) × 100%
In this case:
(15 / 25) × 100% = 0.6 × 100% = 60%
Therefore, 15 is 60% of 25. This percentage representation is often the most intuitive and readily understood way of expressing the relationship between the part and the whole.
Visual Representation: Understanding Proportions
Imagine a pizza cut into 25 equal slices. If you eat 15 slices, you have consumed 15/25 of the pizza. Simplifying this fraction to 3/5 helps visualize that you've eaten 3 out of every 5 slices. This visual representation makes the concept of fractions and ratios more concrete and easier to grasp. Similarly, understanding that you've eaten 60% of the pizza offers a clear and concise representation of the portion consumed.
Real-World Applications: Putting it into Practice
Understanding the relationship between 15 and 25 has numerous practical applications. For example:
-
Sales and Discounts: A store might offer a 60% discount on an item. If the original price is $25, the discount amount would be $15 (60% of $25).
-
Surveys and Statistics: If a survey of 25 people shows that 15 prefer a particular product, this translates to 60% preference for that product.
-
Financial Calculations: Understanding percentages and fractions is crucial for calculating interest, taxes, and other financial aspects. For example, determining the proportion of a loan that has been repaid.
-
Measurement and Conversion: Many conversion problems involve working with fractions and percentages, such as converting units of measurement or determining proportions in recipes.
Expanding the Understanding: Beyond Simple Fractions
While this article focuses on the specific problem of "What is 15 of 25?", the underlying principles can be applied to a much wider range of fractional and percentage problems. Understanding how to simplify fractions, convert them to decimals and percentages, and interpret ratios is fundamental to success in various mathematical and real-world scenarios.
Further Exploration: More Complex Ratios
Let's consider a more complex scenario: What if we wanted to determine what portion of 75 is represented by 45? This problem requires the same principles but with larger numbers:
-
Form the fraction: 45/75
-
Find the GCD: The GCD of 45 and 75 is 15.
-
Simplify the fraction: 45 ÷ 15 = 3; 75 ÷ 15 = 5. The simplified fraction is 3/5.
-
Convert to a decimal: 3 ÷ 5 = 0.6
-
Convert to a percentage: (45/75) × 100% = 60%
Therefore, 45 is 3/5 or 60% of 75. Notice that the simplified fraction and percentage remain the same, highlighting the consistent relationships between these different mathematical representations, even with larger numbers.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to simplify fractions?
A: The easiest way is to find the greatest common divisor (GCD) of the numerator and denominator and then divide both by the GCD. Many calculators have a GCD function, or you can find online tools that calculate the GCD for you. Alternatively, you can systematically divide by common factors until you reach the simplest form.
Q: How can I quickly convert a fraction to a percentage?
A: Divide the numerator by the denominator and then multiply the result by 100%. This gives you the percentage equivalent of the fraction.
Q: Are there any online tools to help with fraction simplification and percentage calculations?
A: Yes, many online calculators and converters are available that can simplify fractions, convert between fractions, decimals, and percentages, and perform other mathematical operations.
Q: Why is understanding percentages important?
A: Percentages are crucial for understanding and comparing proportions in many contexts, such as sales, discounts, statistics, financial calculations, and more. They provide a standardized and easily understandable way to represent parts of a whole.
Conclusion: Mastering Fractions and Percentages
The question "What is 15 of 25?" might appear simple at first glance, but it serves as a gateway to understanding fundamental mathematical concepts such as fractions, ratios, decimals, and percentages. By exploring different methods of solving this problem, we've not only found the answer (3/5, 0.6, or 60%) but also gained a deeper appreciation for the interconnectedness of these mathematical representations. Mastering these concepts is essential for navigating various aspects of daily life and for success in further mathematical studies. Remember, practice is key – the more you work with fractions and percentages, the more comfortable and confident you will become.
Latest Posts
Latest Posts
-
One Thousand And Fifty Dollars
Sep 16, 2025
-
3 4 Divided In Half
Sep 16, 2025
-
How Do You Write 3000
Sep 16, 2025
-
Sum Of Interior Angles Hexagon
Sep 16, 2025
-
2 1 8 In Decimal
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.