What Is 11 Times 12
keralas
Sep 14, 2025 · 7 min read
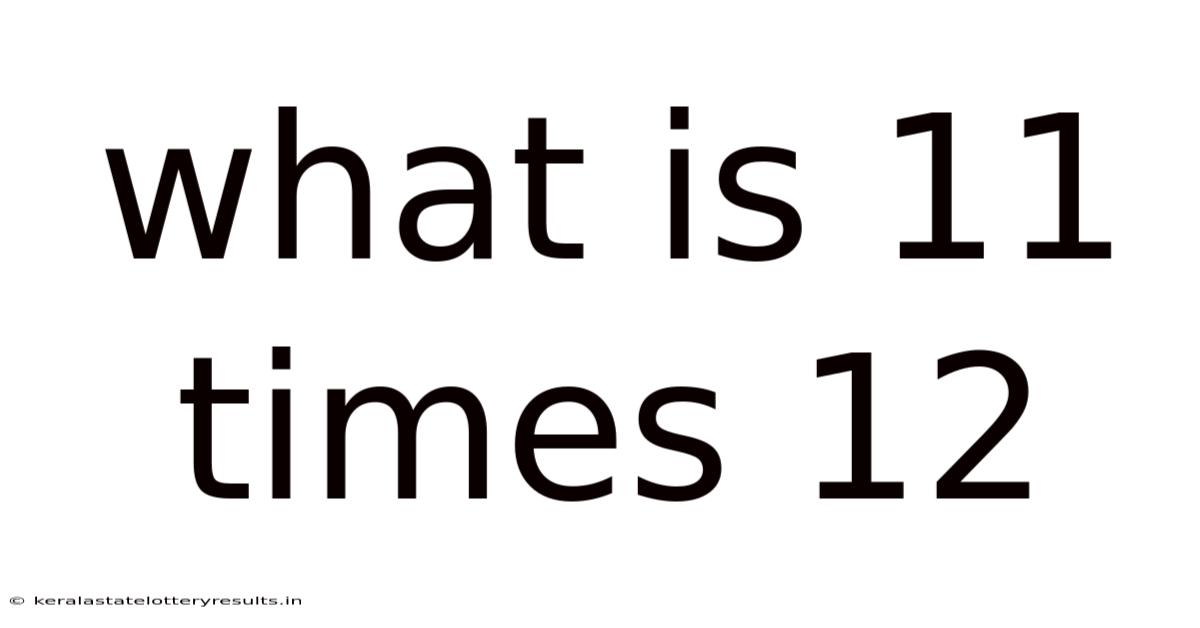
Table of Contents
What is 11 Times 12? Unlocking the Power of Multiplication
This seemingly simple question, "What is 11 times 12?", opens a door to a vast world of mathematical concepts. While the immediate answer might seem trivial, exploring the different methods to solve it reveals fundamental principles of multiplication and lays the groundwork for understanding more complex arithmetic operations. This article will delve into various approaches to calculating 11 x 12, explaining the underlying logic and offering insights that go beyond a simple numerical result. We'll cover everything from basic multiplication techniques to more advanced strategies, exploring the beauty and practicality of mathematics along the way.
I. The Fundamental Approach: Basic Multiplication
The most straightforward way to calculate 11 x 12 is through basic multiplication. We can break this down using the traditional method taught in elementary school:
-
Step 1: Multiply 11 by the units digit of 12 (which is 2): 11 x 2 = 22. Write down '22'.
-
Step 2: Multiply 11 by the tens digit of 12 (which is 1): 11 x 1 = 11. Write this down beneath the '22', but shifted one place to the left, representing the tens place.
-
Step 3: Add the two results:
11
x 12
----
22
110
----
132
Therefore, 11 times 12 equals 132.
This method is intuitive and easily grasped, making it a cornerstone of early mathematical education. It highlights the distributive property of multiplication, breaking down the problem into smaller, manageable parts.
II. The Distributive Property: A Deeper Dive
The previous method implicitly used the distributive property, a fundamental concept in algebra. The distributive property states that for any numbers a, b, and c: a(b + c) = ab + ac.
In our case, we can rewrite 11 x 12 as 11 x (10 + 2). Applying the distributive property:
11 x (10 + 2) = (11 x 10) + (11 x 2) = 110 + 22 = 132
This approach demonstrates the underlying principle behind the traditional multiplication method. Understanding the distributive property is crucial for more advanced mathematical concepts.
III. The Lattice Method: A Visual Approach
The lattice method provides a visual and organized way to perform multiplication. It's particularly helpful for larger numbers. Here's how it works for 11 x 12:
-
Draw a grid: Create a 2x2 grid (because both numbers have two digits).
-
Divide the grid: Divide each cell diagonally.
-
Multiply and place: Multiply each digit combination and place the result in the corresponding cell, with the tens digit above the diagonal and the units digit below.
1 | 1
-------+-------
| 2 | 2
-------+-------
| |
1 | 1
-------+-------
2 | 2
-------+-------
- Add diagonally: Sum the numbers along the diagonals, starting from the bottom right. Carry-over any tens to the next diagonal.
1 | 1
-------+-------
2 | 2
-------+-------
2 | 3 | 2
The result, read from top left to bottom right, is 132.
The lattice method provides a structured approach that minimizes the chance of errors, particularly for those who find carrying-over digits in traditional multiplication challenging.
IV. Using the Difference of Squares: An Elegant Alternative
This method employs a clever algebraic trick using the difference of squares. We can express 11 as (10 + 1) and 12 as (10 + 2). The difference of squares formula states: (a + b)(a - b) = a² - b².
While this doesn't directly solve 11 x 12, it can be used in a related calculation. Let's consider (12 - 1) x (12 + 1) = 11 x 13. This equals 12² - 1² = 144 - 1 = 143. Knowing this, we can use a slightly altered approach.
We know that 11 x 11 = 121 and 11 x 13 = 143. Observing the pattern, we see that moving from 11 x 11 to 11 x 13 adds 22. Since we need to find 11 x 12, which is in between, we subtract 11 from 143, resulting in 132. It's a bit more roundabout, but it demonstrates the power of applying algebraic principles to solve arithmetic problems.
V. Mental Math Techniques: Speed and Efficiency
For those who wish to boost their mental calculation skills, several techniques can efficiently calculate 11 x 12 without pen and paper.
-
Distributive property (mental approach): Mentally calculate 11 x 10 = 110 and 11 x 2 = 22. Add them together: 110 + 22 = 132.
-
Breaking down the numbers: Calculate 10 x 12 = 120. Then add 12 (1 x 12): 120 + 12 = 132. This is essentially applying the distributive property.
-
Using patterns: Notice that multiplying by 11 often involves a pattern (especially for two-digit numbers). For example, 11 x 12 can be seen as adding 12 to itself shifted one place to the left: 12 + 120 = 132. This pattern is not always easily applied but can be beneficial with practice.
Mastering these mental math techniques enhances mathematical fluency and problem-solving abilities.
VI. The Significance of 132: Exploring Connections
The answer, 132, is itself a number with interesting mathematical properties.
-
It's a composite number: Meaning it has factors other than 1 and itself (1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132).
-
It's divisible by many small numbers: Its divisibility by 2, 3, 4, 6, and 11 highlights its composite nature.
-
It's an abundant number: The sum of its proper divisors (divisors excluding itself) is greater than 132.
These properties showcase the rich tapestry of number theory and the various relationships between numbers. Exploring such connections deepens mathematical understanding and fosters appreciation for the elegance of mathematics.
VII. Beyond the Basics: Applications in Real Life
While this might seem like a simple calculation, understanding multiplication is crucial for countless everyday applications. From calculating the total cost of multiple items to determining the area of a room, multiplication forms the bedrock of numerous practical calculations. Consider these examples:
-
Shopping: If you buy 11 items costing $12 each, you'll spend 11 x $12 = $132.
-
Construction: If you are laying tiles on a floor measuring 11 feet by 12 feet, you need 132 square feet of tiles.
-
Cooking: If a recipe calls for 11 ounces of an ingredient for each of 12 servings, you'll need 132 ounces of the ingredient.
These examples illustrate the practical significance of multiplication in daily life, emphasizing that this simple calculation underlies many complex problems.
VIII. Frequently Asked Questions (FAQs)
Q1: Are there other ways to calculate 11 x 12?
A1: Yes, numerous methods exist, as demonstrated throughout this article. The choice of method often depends on personal preference, the available tools, and the context of the problem.
Q2: Why is understanding the distributive property important?
A2: The distributive property is fundamental in algebra and forms the basis for many advanced mathematical concepts. Understanding it provides a deeper insight into the underlying principles of arithmetic operations.
Q3: What are some strategies for improving mental math skills?
A3: Practice, breaking down problems into smaller parts, and memorizing multiplication tables are all helpful strategies for improving mental math skills. Regular practice is key.
Q4: Is there a connection between 11 x 12 and other mathematical concepts?
A4: Absolutely! As mentioned earlier, 132 has various mathematical properties that connect it to number theory and other related fields. Exploring these connections enhances mathematical intuition and appreciation.
IX. Conclusion: More Than Just an Answer
The seemingly simple question, "What is 11 times 12?", has led us on a journey through different approaches to multiplication, exploring fundamental mathematical principles and their practical applications. While the answer, 132, is straightforward, the process of arriving at it reveals a wealth of knowledge and illuminates the beauty and power of mathematics. This article hopefully demonstrates that mathematical concepts are not just abstract theories but practical tools applicable to various aspects of our lives. By understanding the various methods and their underlying principles, we not only solve the problem but also cultivate a deeper appreciation for the elegance and usefulness of mathematics.
Latest Posts
Latest Posts
-
Adjacent Angles Are Always Supplementary
Sep 14, 2025
-
Find Derivative Of An Integral
Sep 14, 2025
-
What Are The Factors 72
Sep 14, 2025
-
Different Types Of Scatter Graphs
Sep 14, 2025
-
Is 397 A Prime Number
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 11 Times 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.