Square Root Of 10 000
keralas
Sep 16, 2025 · 5 min read
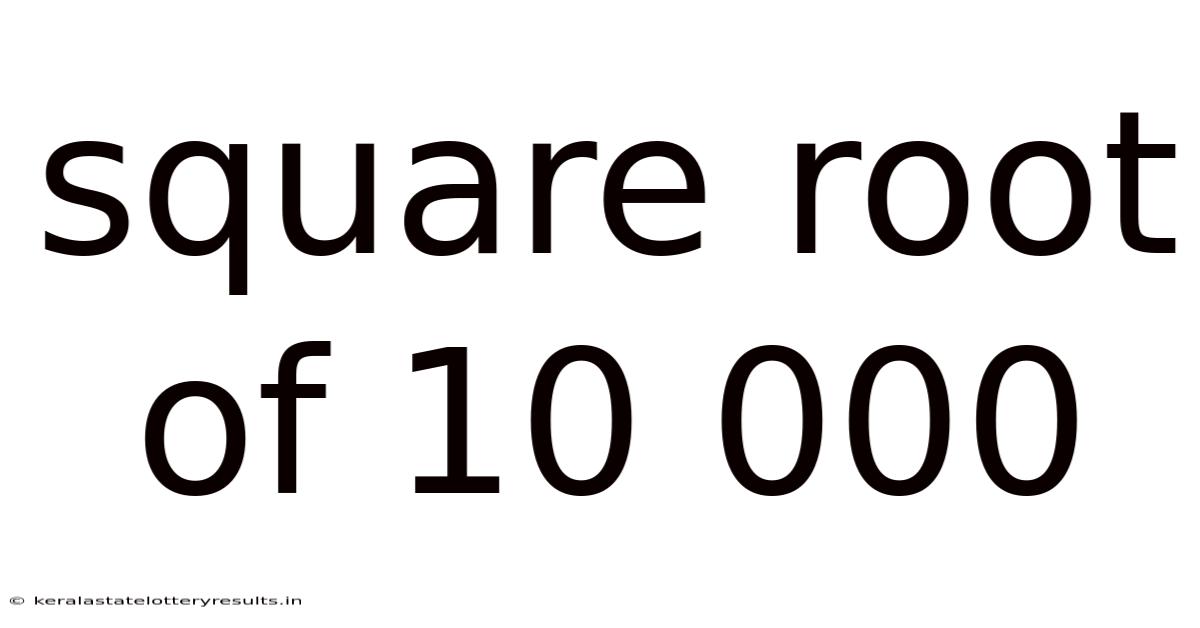
Table of Contents
Unveiling the Mystery: Understanding the Square Root of 10,000
Finding the square root of 10,000 might seem like a simple mathematical task, especially for those familiar with basic arithmetic. However, delving deeper reveals a fascinating connection between this seemingly straightforward calculation and broader mathematical concepts. This article will not only provide the answer but also explore the underlying principles, different methods of calculation, and real-world applications, making the concept accessible and engaging for all readers. Understanding square roots is fundamental to various fields, from geometry and physics to computer science and finance.
Understanding Square Roots: A Foundation
Before we tackle the square root of 10,000, let's solidify our understanding of what a square root actually is. A square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. We represent the square root using the radical symbol (√). Therefore, √9 = 3.
This concept can be extended to larger numbers. The square root of 10,000 is the number that, when multiplied by itself, equals 10,000. This might seem daunting at first, but we'll explore various methods to efficiently find the solution.
Calculating the Square Root of 10,000: Methods and Approaches
Several methods exist for calculating the square root of 10,000. Let's examine a few:
1. Prime Factorization:
This method is particularly useful for understanding the underlying structure of the number. We begin by breaking down 10,000 into its prime factors:
10,000 = 10 x 10 x 10 x 10 = (2 x 5) x (2 x 5) x (2 x 5) x (2 x 5) = 2⁴ x 5⁴
Notice the pattern: we have four 2's and four 5's. When we take the square root, we essentially halve the exponents:
√(2⁴ x 5⁴) = 2² x 5² = 4 x 25 = 100
Therefore, the square root of 10,000 is 100.
2. Estimation and Iteration (Babylonian Method):
This ancient method provides an iterative approach to finding increasingly accurate approximations. We start with an initial guess and refine it through repeated calculations. Let's begin with a guess of 100:
- Step 1: Divide 10,000 by our guess (100): 10,000 / 100 = 100
- Step 2: Average the guess and the result from Step 1: (100 + 100) / 2 = 100
In this case, our initial guess was already accurate. The Babylonian method converges quickly towards the correct answer, especially with a good initial estimate. For more complex numbers, several iterations might be required.
3. Using a Calculator:
Modern calculators are designed to handle square root calculations effortlessly. Simply input 10,000 and press the square root button (√) to obtain the answer: 100. While this is the fastest method, it doesn't provide the same level of understanding as the previous methods.
4. Recognizing Perfect Squares:
This is the most efficient method for simple perfect squares like 10,000. Perfect squares are numbers that are the product of an integer multiplied by itself. Familiarity with perfect squares allows for immediate recognition. Since 10 x 10 = 100, and 100 x 100 = 10,000, we can immediately deduce that the square root of 10,000 is 100.
Beyond the Calculation: Applications and Significance
The square root of 10,000, and the broader concept of square roots, finds applications in diverse fields:
-
Geometry: Calculating the side length of a square given its area. If a square has an area of 10,000 square units, its side length is √10,000 = 100 units. This principle extends to other geometric shapes and calculations involving area and volume.
-
Physics: Many physical phenomena involve squared relationships. For instance, the kinetic energy of an object is proportional to the square of its velocity. Understanding square roots is crucial for solving equations related to energy, motion, and other physical properties.
-
Computer Science: Square roots are frequently used in algorithms and computational processes, particularly in graphics processing, game development, and simulations. Efficient square root calculations are essential for optimizing performance in these applications.
-
Finance: Calculating compound interest, analyzing investment returns, and assessing risk often involve square roots. Understanding this mathematical concept is crucial for financial modeling and decision-making.
-
Statistics: Square roots are used in calculating standard deviation, a key measure of data dispersion. This concept underpins statistical analysis and interpretation across various fields.
Frequently Asked Questions (FAQ)
-
Q: Is there a negative square root of 10,000?
- A: Technically, yes. (-100) x (-100) = 10,000. However, when we talk about the square root, we typically refer to the principal square root, which is the non-negative value (100).
-
Q: How can I calculate the square root of a number without a calculator?
- A: The Babylonian method, prime factorization, and estimation techniques provide methods for approximating square roots without relying on a calculator. The accuracy of the approximation depends on the method and the number of iterations.
-
Q: What if I need to find the square root of a non-perfect square?
- A: For non-perfect squares, you'll need to use approximation methods like the Babylonian method or a calculator. You can also use logarithms or specialized algorithms for more precise results.
Conclusion: More Than Just a Number
The square root of 10,000, while seemingly simple at first glance, opens a gateway to understanding fundamental mathematical concepts with wide-ranging practical applications. From simple geometric calculations to complex algorithms in computer science and finance, the ability to grasp and apply the concept of square roots is invaluable. This article aimed not only to provide the answer (100) but also to illuminate the underlying principles and demonstrate the diverse ways in which this fundamental concept contributes to our understanding of the world around us. By exploring different methods of calculation and highlighting real-world examples, we hope to have fostered a deeper appreciation for this often-overlooked cornerstone of mathematics. Remember, the journey of understanding is often more rewarding than simply arriving at the answer.
Latest Posts
Latest Posts
-
Area Of Irregular Shapes Worksheet
Sep 16, 2025
-
Gcf Of 56 And 24
Sep 16, 2025
-
Simplify Square Root Of 35
Sep 16, 2025
-
Is 11 Prime Or Composite
Sep 16, 2025
-
How To Find Relative Min
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 10 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.