Simplify X 2 X 3
keralas
Sep 17, 2025 · 5 min read
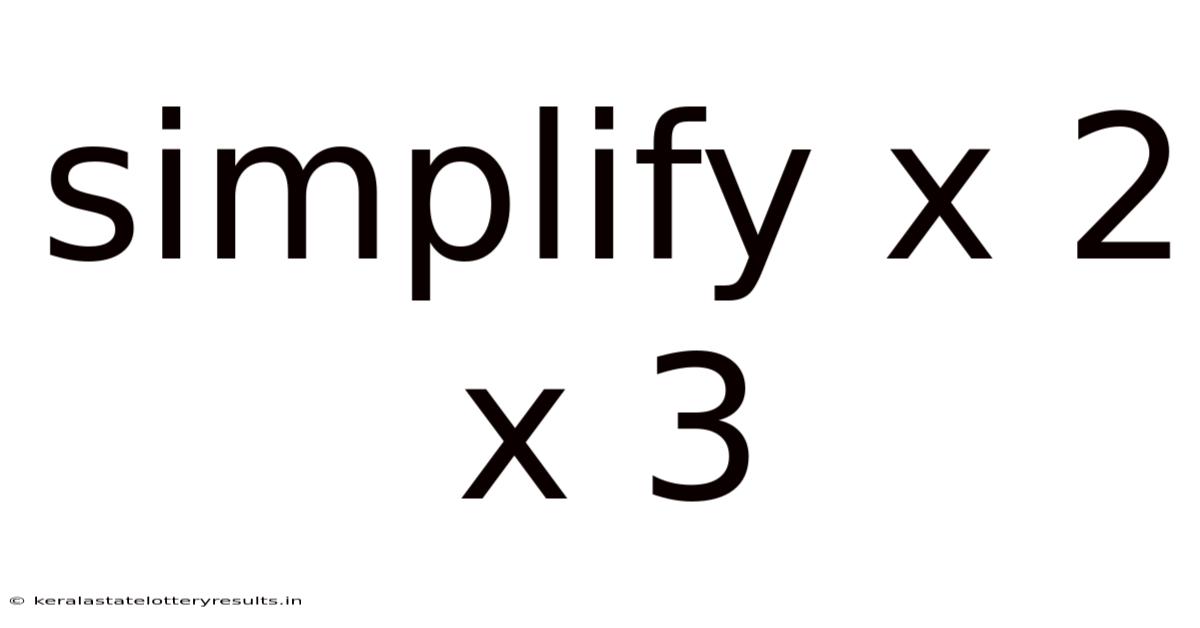
Table of Contents
Simplifying x² x ³: A Deep Dive into Algebraic Multiplication
Understanding how to simplify algebraic expressions is fundamental to success in mathematics, particularly algebra and beyond. This article will comprehensively explore the simplification of the expression x² x ³, explaining the underlying principles, providing step-by-step solutions, and delving into the broader mathematical concepts involved. We'll move beyond a simple answer and delve into the "why" behind the methods, making this a valuable resource for students of all levels.
Introduction: Understanding the Basics
The expression x² x ³ involves the multiplication of two terms containing the same variable, x, raised to different powers. Simplifying this expression relies on the fundamental rules of exponents, specifically the rule for multiplying terms with the same base. This seemingly simple expression provides a perfect springboard to understand more complex algebraic manipulations. Mastering this concept lays the groundwork for tackling polynomials, equations, and more advanced algebraic concepts.
Step-by-Step Simplification: The Power of Exponents
The core principle in simplifying x² x ³ lies in understanding how exponents work. An exponent indicates how many times a base number is multiplied by itself. In our expression, x² means x multiplied by itself twice (x * x), and x³ means x multiplied by itself three times (x * x * x).
Therefore, x² x ³ can be written as:
(x * x) * (x * x * x)
Combining these factors, we get:
x * x * x * x * x
This is equivalent to x raised to the power of 5, or x⁵.
Therefore, the simplified expression is x⁵.
The Rule of Exponents for Multiplication:
The process above demonstrates a general rule of exponents: when multiplying terms with the same base, you add the exponents. Formally, this is expressed as:
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
In our case, a = 2 and b = 3, so x² * x³ = x⁽²⁺³⁾ = x⁵. This rule is crucial for simplifying numerous algebraic expressions.
Beyond the Basics: Expanding the Understanding
While the simplification of x² x ³ is straightforward, understanding the underlying principles allows us to tackle more complex scenarios. Let's explore some related concepts:
-
Different Bases: The rule of adding exponents only applies when the bases are the same. For instance, x² * y³ cannot be simplified further because the bases (x and y) are different.
-
Negative Exponents: The rule still holds true even if the exponents are negative. For example, x⁻² * x³ = x⁽⁻²⁺³⁾ = x¹. Remember that x¹ = x.
-
Fractional Exponents: The rule also applies to fractional exponents (exponents that are fractions). For example, x^(1/2) * x^(1/2) = x⁽¹/²⁺¹/²⁾ = x¹.
-
Zero Exponents: Any base raised to the power of zero equals 1 (except for 0⁰, which is undefined). For example, x⁰ = 1. This can be incorporated into our multiplication rule: x² * x⁰ = x⁽²⁺⁰⁾ = x².
-
Coefficient Multiplication: Often, algebraic terms will include coefficients (numbers multiplied by the variables). For example, 2x² * 3x³. In this case, you multiply the coefficients and add the exponents of the variables: (2 * 3) * x⁽²⁺³⁾ = 6x⁵.
Real-World Applications and Problem Solving
Understanding how to simplify expressions like x² x ³ is not merely an abstract mathematical exercise; it has wide-ranging applications in various fields. Some examples include:
-
Physics: Many physical laws and equations are expressed algebraically. Simplifying expressions is crucial for solving for unknowns and making calculations more efficient. For example, calculating the area of a square with side length x² requires understanding how to work with exponents.
-
Engineering: Engineers frequently use algebraic manipulations to design and analyze systems. Simplifying complex expressions is vital for making accurate calculations and predictions. Consider the volume calculations in civil engineering or electrical current calculations in electrical engineering.
-
Computer Science: In programming, understanding algebraic manipulation is important for optimizing code and improving efficiency. Data structures and algorithms frequently involve algebraic expressions and their manipulation.
-
Finance: Financial modeling and analysis often involve complex formulas and equations. The ability to simplify expressions can greatly aid in making accurate financial predictions.
Frequently Asked Questions (FAQs)
-
Q: What happens if I subtract the exponents instead of adding them?
- A: Subtracting exponents is used when dividing terms with the same base, not multiplying. The rule for division is xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾.
-
Q: Can I simplify x² + x³?
- A: No. Addition and subtraction of algebraic terms require like terms. x² and x³ are not like terms (they have different exponents), so they cannot be combined using addition or subtraction.
-
Q: What if I have more than two terms to multiply?
- A: The rule of adding exponents applies to any number of terms with the same base. For example, x² * x³ * x⁴ = x⁽²⁺³⁺⁴⁾ = x⁹.
-
Q: What if there are parentheses involved?
- A: If parentheses are used for grouping, perform the operations within the parentheses first, then apply the rule for multiplying terms with the same base. For instance, (x²) (x³) = x⁵. However, (x²+x)(x³) is different. Here, you must use the distributive property to expand.
Conclusion: Mastering the Fundamentals
Simplifying x² x ³, while seemingly basic, is a crucial stepping stone in mastering algebra. Understanding the underlying rules of exponents—specifically the rule for multiplying terms with the same base—opens doors to solving more complex algebraic problems. This knowledge is not just confined to the classroom; its application extends to various disciplines, highlighting the practical importance of these fundamental mathematical concepts. By grasping these principles, you build a strong foundation for further mathematical explorations. Continue practicing with various examples, including those involving coefficients, negative exponents, and fractional exponents to solidify your understanding and confidence in algebraic simplification. Remember, consistent practice is key to mastering these essential algebraic skills.
Latest Posts
Latest Posts
-
Integration Of X Log X
Sep 17, 2025
-
What Is The Missing Number
Sep 17, 2025
-
What Is 1 2 In Decimals
Sep 17, 2025
-
Square Root Of An Equation
Sep 17, 2025
-
At Least Sign For Inequalities
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Simplify X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.