Lcm Of 25 Qnd 10
keralas
Sep 14, 2025 · 6 min read
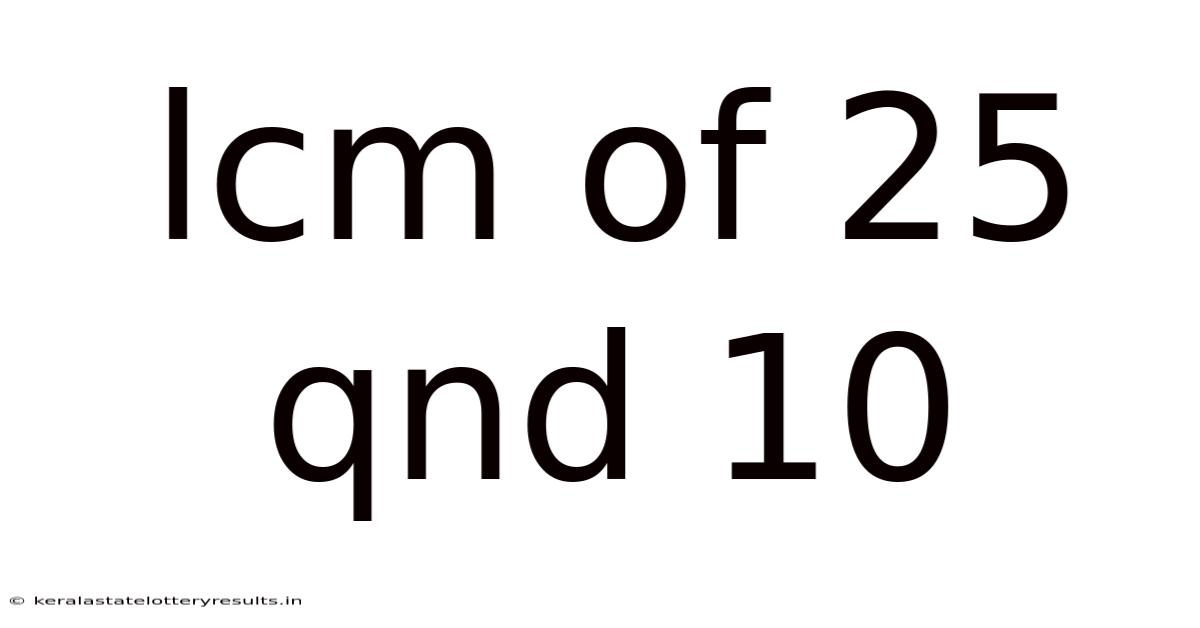
Table of Contents
Finding the Least Common Multiple (LCM) of 25 and 10: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving problems in algebra and beyond. This article provides a comprehensive guide to calculating the LCM of 25 and 10, exploring different methods and illustrating the underlying principles. We'll delve into the definition of LCM, explore several calculation techniques, and even look at the theoretical underpinnings to ensure a thorough understanding. This guide is perfect for students learning about LCM for the first time, as well as those needing a refresher on this important mathematical concept.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 25 and 10, let's define what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both of your chosen numbers can divide into evenly. For instance, multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The least common multiple of 2 and 3 is 6 because it's the smallest number that appears in both lists.
This concept extends to any number of integers, but for this article, we'll focus on finding the LCM of just two numbers: 25 and 10.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 25 and 10, involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70...
- Multiples of 25: 25, 50, 75, 100, 125...
By comparing the lists, we can see that the smallest number that appears in both lists is 50. Therefore, the LCM of 25 and 10 is 50. This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM from those prime factors.
Step 1: Prime Factorization
Let's find the prime factorization of 25 and 10.
- 25: 25 can be factored as 5 x 5, or 5².
- 10: 10 can be factored as 2 x 5.
Step 2: Constructing the LCM
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together.
In our case:
- The prime factors are 2 and 5.
- The highest power of 2 is 2¹ (from the factorization of 10).
- The highest power of 5 is 5² (from the factorization of 25).
Therefore, the LCM(25, 10) = 2¹ x 5² = 2 x 25 = 50.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a simple formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers and |a x b| represents the absolute value of their product.
Step 1: Finding the GCD
To use this method, we first need to find the greatest common divisor (GCD) of 25 and 10. The GCD is the largest number that divides both 25 and 10 without leaving a remainder. We can find this using the Euclidean algorithm or by listing the divisors.
- Divisors of 25: 1, 5, 25
- Divisors of 10: 1, 2, 5, 10
The largest common divisor is 5. Therefore, GCD(25, 10) = 5.
Step 2: Calculating the LCM
Now, we can use the formula:
LCM(25, 10) = (|25 x 10|) / GCD(25, 10) = 250 / 5 = 50
This method confirms that the LCM of 25 and 10 is 50.
Comparing the Methods
All three methods yield the same result: the LCM of 25 and 10 is 50. However, each method has its strengths and weaknesses:
- Listing Multiples: Simple and intuitive for smaller numbers, but inefficient for larger numbers.
- Prime Factorization: More efficient and provides a deeper understanding of number theory, suitable for larger numbers.
- Using GCD: Elegant and efficient, especially when the GCD is easily determined.
Applications of LCM
Understanding and calculating the LCM has numerous applications in various areas of mathematics and beyond:
- Fractions: Finding the LCM is crucial when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator.
- Scheduling: LCM is used to solve problems related to scheduling events that occur at regular intervals (e.g., determining when two events will occur simultaneously).
- Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
- Music Theory: LCM is used to determine the least common multiple of rhythmic patterns.
Frequently Asked Questions (FAQ)
Q1: What if one of the numbers is 0?
The LCM of any number and 0 is undefined because 0 has infinitely many multiples.
Q2: Can the LCM of two numbers be one of the numbers themselves?
Yes, if one number is a multiple of the other, the LCM will be the larger number. For example, LCM(10, 20) = 20.
Q3: Is there a method to find the LCM of more than two numbers?
Yes, you can extend the prime factorization method or the GCD method to find the LCM of more than two numbers. For prime factorization, you would consider the highest power of each prime factor present in any of the factorizations. For the GCD method, you would iteratively compute the LCM of pairs of numbers.
Q4: Why is the prime factorization method considered more efficient for larger numbers?
The prime factorization method is more efficient because it avoids the potentially lengthy process of listing all multiples. It directly utilizes the fundamental building blocks of numbers (prime factors) to construct the LCM.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with broad applications. This article explored three different methods – listing multiples, prime factorization, and using the GCD – for calculating the LCM, demonstrating their strengths and weaknesses. We've shown how to find the LCM of 25 and 10 using each method, revealing that the answer is 50. Understanding these methods allows you to tackle more complex problems involving LCM, strengthening your mathematical foundation and opening up a deeper appreciation for number theory. Remember to choose the method best suited for the numbers you are working with, prioritizing efficiency and understanding. The key takeaway is to master the underlying principles, allowing you to confidently tackle LCM problems in various contexts.
Latest Posts
Latest Posts
-
How Much Is 100 Km
Sep 14, 2025
-
Simplify Square Root Of 85
Sep 14, 2025
-
Algebra Problems For 4th Graders
Sep 14, 2025
-
How To Spell 50 Dollars
Sep 14, 2025
-
How Much Is 100 Mm
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 25 Qnd 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.