Lcm Of 12 15 10
keralas
Sep 13, 2025 · 6 min read
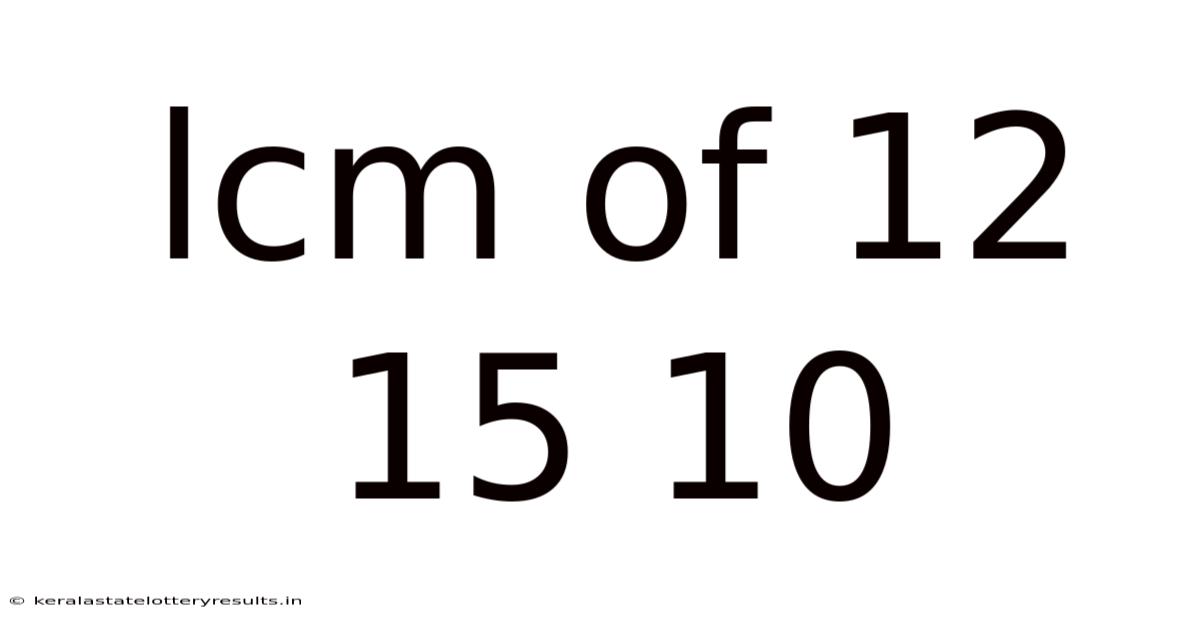
Table of Contents
Finding the Least Common Multiple (LCM) of 12, 15, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and different methods for calculating it is crucial for various mathematical applications, from simplifying fractions to solving problems involving cycles and rhythms. This comprehensive guide will explore the LCM of 12, 15, and 10, explaining multiple approaches and delving into the theoretical foundations. We'll cover everything from basic methods suitable for beginners to more advanced techniques, ensuring a thorough understanding for learners of all levels.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 12, 15, and 10, let's establish a solid understanding of the concept itself. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the given numbers. In simpler terms, it's the smallest number that can be divided evenly by all the numbers in the set. Understanding LCM is essential in various areas, including:
- Fraction Arithmetic: Finding the LCM of the denominators is crucial when adding or subtracting fractions with different denominators.
- Scheduling and Cycles: Determining when events with different periodicities will coincide (e.g., the timing of planetary alignments or the overlapping of work schedules).
- Modular Arithmetic: LCM plays a significant role in solving problems related to congruences and modular systems.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, ...
By comparing the lists, we can see that the smallest number common to all three lists is 60. Therefore, the LCM of 12, 15, and 10 is 60.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It relies on expressing each number as a product of its prime factors. Prime factorization is the process of breaking down a number into its prime number components.
- Prime Factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Prime Factorization of 15: 15 = 3 x 5
- Prime Factorization of 10: 10 = 2 x 5
Next, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2².
- The highest power of 3 is 3.
- The highest power of 5 is 5.
To find the LCM, we multiply these highest powers together: 2² x 3 x 5 = 4 x 3 x 5 = 60
This method is more systematic and generally faster than listing multiples, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
There's a useful relationship between the LCM and the greatest common divisor (GCD) of two numbers:
LCM(a, b) * GCD(a, b) = a * b
While this formula directly applies to two numbers, we can extend it to multiple numbers by applying it iteratively. First, let's find the GCD of 12 and 15 using the Euclidean algorithm:
- Divide 15 by 12: 15 = 12 x 1 + 3
- Divide 12 by the remainder 3: 12 = 3 x 4 + 0
The GCD of 12 and 15 is 3. Now, let's find the LCM(12, 15):
LCM(12, 15) = (12 * 15) / GCD(12, 15) = (180) / 3 = 60
Now we repeat the process with the LCM(12,15) and 10:
First find the GCD(60,10):
- Divide 60 by 10: 60 = 10 x 6 +0 The GCD(60,10) is 10.
Now find the LCM(60,10): LCM(60, 10) = (60 * 10) / GCD(60, 10) = 600/10 = 60
Therefore, the LCM of 12, 15, and 10 is 60. This method demonstrates the interconnectedness of GCD and LCM.
Method 4: Using the Least Common Multiple Calculator (Illustrative Only)
While this article avoids external links, it's worth mentioning that online LCM calculators exist. These calculators can quickly compute the LCM for any set of numbers. However, understanding the underlying methods remains crucial for problem-solving and a deeper grasp of mathematical concepts. Using a calculator without understanding the principles behind it limits your ability to apply the concept in different contexts.
Real-World Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. Here are some real-world examples demonstrating its practical applications:
-
Scheduling: Imagine you have three different machines that need maintenance. Machine A requires maintenance every 12 days, Machine B every 15 days, and Machine C every 10 days. To schedule maintenance efficiently, you'd need to find the LCM (60 days). This is the first time all three machines will require maintenance simultaneously.
-
Music: In music theory, the LCM helps determine when different musical phrases or rhythms will align. For instance, if you have a musical phrase with a 12-beat cycle, another with a 15-beat cycle, and a third with a 10-beat cycle, the LCM (60 beats) represents the shortest time interval where all three phrases will simultaneously return to their starting points.
-
Construction: LCM helps in aligning construction materials of different lengths or patterns seamlessly. If you're using bricks of three different lengths (12 units, 15 units, and 10 units), finding the LCM will help determine the smallest length required to ensure a continuous and consistent pattern without any cuts or gaps.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest number divisible by all the given numbers, while the greatest common divisor (GCD) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related; a larger GCD implies a smaller LCM, and vice versa.
Q: Can the LCM of a set of numbers be one of the numbers in the set?
A: Yes, this happens if one of the numbers is a multiple of all the others. For example, the LCM of 2, 4, and 8 is 8.
Q: What if I have more than three numbers?
A: The methods described above can be extended to any number of integers. For the prime factorization method, you simply include all prime factors with their highest powers. For the iterative GCD approach, you calculate the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
Q: Why is the prime factorization method considered more efficient for larger numbers?
A: The listing method becomes impractical for large numbers, as the number of multiples to check significantly increases. Prime factorization provides a systematic approach that doesn't require listing all multiples, making it significantly faster and more efficient, particularly when dealing with large prime numbers.
Conclusion
Finding the least common multiple (LCM) of 12, 15, and 10, which we found to be 60, involves applying fundamental mathematical concepts with broad applications. This article has explored various methods, from the simple listing of multiples to the more sophisticated prime factorization and GCD-based approaches. Understanding these different methods and their underlying principles is not only crucial for solving mathematical problems but also for appreciating the practical implications of LCM in various real-world scenarios, from scheduling and construction to music and beyond. Mastering the concept of LCM provides a solid foundation for further mathematical exploration and problem-solving abilities.
Latest Posts
Latest Posts
-
What Is 20 Off 120
Sep 13, 2025
-
What Are Factors Of 93
Sep 13, 2025
-
Gcf Of 20 And 25
Sep 13, 2025
-
Adjacent Angles Of A Parallelogram
Sep 13, 2025
-
Gcf Of 2 And 4
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 15 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.