Is 7 An Even Number
keralas
Sep 13, 2025 · 6 min read
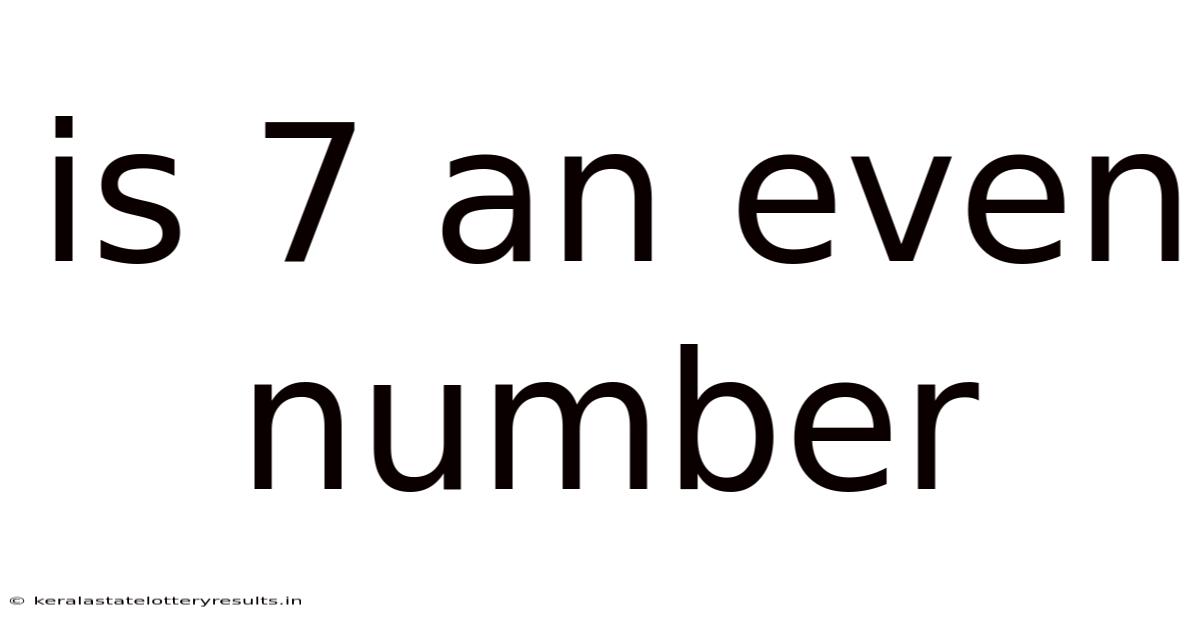
Table of Contents
Is 7 an Even Number? Unraveling the Mystery of Even and Odd Numbers
Is 7 an even number? The answer, quite simply, is no. Seven is an odd number. This seemingly straightforward question opens the door to a deeper exploration of number theory, the fundamental building blocks of mathematics, and the concepts of even and odd numbers themselves. This article will delve into why 7 is odd, explore the definitions of even and odd numbers, explain their properties, and address common misconceptions surrounding these basic yet crucial mathematical concepts.
Understanding Even and Odd Numbers: The Foundation
Before we definitively answer whether 7 is even, let's establish a clear understanding of what constitutes an even and an odd number. These classifications are based on divisibility by 2.
-
Even numbers: An even number is any integer (whole number) that is perfectly divisible by 2, leaving no remainder. This means that when you divide an even number by 2, the result is another whole number. Examples of even numbers include 2, 4, 6, 8, 10, and so on. Mathematically, we can represent an even number as 2n, where 'n' is any integer.
-
Odd numbers: An odd number is any integer that is not divisible by 2. When an odd number is divided by 2, the result will always have a remainder of 1. Examples include 1, 3, 5, 7, 9, and so on. We can represent an odd number mathematically as 2n + 1, where 'n' is again any integer.
The distinction between even and odd numbers is a fundamental concept in elementary arithmetic and forms the basis for understanding more complex mathematical principles later on.
Why 7 is Definitely Odd
Now, let's apply these definitions to the number 7. If we attempt to divide 7 by 2, we get 3 with a remainder of 1. This immediately confirms that 7 does not fit the definition of an even number. It leaves a remainder, violating the requirement for perfect divisibility by 2. Conversely, 7 perfectly satisfies the definition of an odd number: it can be expressed in the form 2n + 1 (where n = 3). Therefore, 7 is undeniably an odd number.
Exploring the Properties of Even and Odd Numbers
Understanding the properties of even and odd numbers can enhance mathematical intuition and problem-solving skills. Here are some key properties:
- Sum of two even numbers: The sum of two even numbers is always an even number. (e.g., 2 + 4 = 6)
- Sum of two odd numbers: The sum of two odd numbers is always an even number. (e.g., 3 + 5 = 8)
- Sum of an even and an odd number: The sum of an even and an odd number is always an odd number. (e.g., 2 + 3 = 5)
- Product of two even numbers: The product of two even numbers is always an even number. (e.g., 2 x 4 = 8)
- Product of two odd numbers: The product of two odd numbers is always an odd number. (e.g., 3 x 5 = 15)
- Product of an even and an odd number: The product of an even and an odd number is always an even number. (e.g., 2 x 3 = 6)
These properties are not merely arbitrary observations; they are direct consequences of the definitions of even and odd numbers and their divisibility by 2. Understanding these properties is crucial for simplifying calculations and solving various mathematical problems.
Beyond the Basics: Even and Odd Numbers in Higher Mathematics
The seemingly simple distinction between even and odd numbers extends far beyond elementary arithmetic. These concepts play a significant role in various advanced mathematical fields, including:
-
Number Theory: Even and odd numbers are fundamental in exploring number properties, prime numbers, and modular arithmetic. Concepts like parity (whether a number is even or odd) are extensively used in proving theorems and solving complex number-theoretic problems.
-
Abstract Algebra: The concepts of evenness and oddness extend to more abstract algebraic structures, where elements can be classified based on analogous properties.
-
Combinatorics and Graph Theory: Parity often plays a crucial role in combinatorial problems and graph theory, helping determine the existence or non-existence of certain structures or solutions.
-
Cryptography: The properties of even and odd numbers are surprisingly relevant in cryptography, where they can contribute to designing secure encryption and decryption algorithms.
While the application may be less immediate than basic arithmetic, the foundational concept remains the same: the divisibility, or lack thereof, by 2.
Addressing Common Misconceptions
Despite their simplicity, some common misconceptions surround even and odd numbers. Let's address a few:
-
Zero is an even number: This is often a point of confusion. Zero is indeed an even number because it is divisible by 2 with a remainder of 0 (0/2 = 0).
-
Negative numbers can be even or odd: Negative numbers can also be classified as either even or odd. For example, -2, -4, -6 are even, and -1, -3, -5 are odd. The rules of divisibility by 2 apply to negative integers as well.
-
Fractions and decimals are neither even nor odd: The classification of even and odd applies only to integers (whole numbers). Fractions and decimals cannot be categorized as even or odd.
Frequently Asked Questions (FAQ)
Q: Is 7 a prime number?
A: Yes, 7 is a prime number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. 7 is only divisible by 1 and 7.
Q: What is the next odd number after 7?
A: The next odd number after 7 is 9.
Q: How can I quickly determine if a large number is even or odd?
A: Look at the last digit. If the last digit is 0, 2, 4, 6, or 8, the number is even. If the last digit is 1, 3, 5, 7, or 9, the number is odd.
Q: Are there infinitely many even and odd numbers?
A: Yes, there are infinitely many even and odd numbers. The sequence of integers extends infinitely in both positive and negative directions.
Q: What is the significance of even and odd numbers in real-world applications?
A: Even and odd numbers have practical applications in various fields. For instance, in computer science, parity bits are used for error detection in data transmission, relying on the concept of even and odd numbers. In scheduling and resource allocation, even and odd numbers can help create balanced distributions or alternating patterns.
Conclusion: The Simple Truth About 7
In conclusion, the answer to the question "Is 7 an even number?" is a resounding no. Seven is unequivocally an odd number. This seemingly simple question serves as a gateway to understanding the fundamental concepts of even and odd numbers, their properties, and their far-reaching implications in various branches of mathematics and beyond. By grasping the definitions and properties of even and odd numbers, we build a stronger foundation for exploring more complex mathematical concepts and appreciating the elegance and interconnectedness of mathematical principles. The seemingly simple concept of parity underlies a vast and fascinating area of mathematical study.
Latest Posts
Latest Posts
-
Is 52 Prime Or Composite
Sep 13, 2025
-
Gcf Of 75 And 100
Sep 13, 2025
-
Factorise X 2 5x 6
Sep 13, 2025
-
What Is 80 Degrees C
Sep 13, 2025
-
Integration Of X Cos X
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 7 An Even Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.