Integration Of X Log X
keralas
Sep 17, 2025 · 6 min read
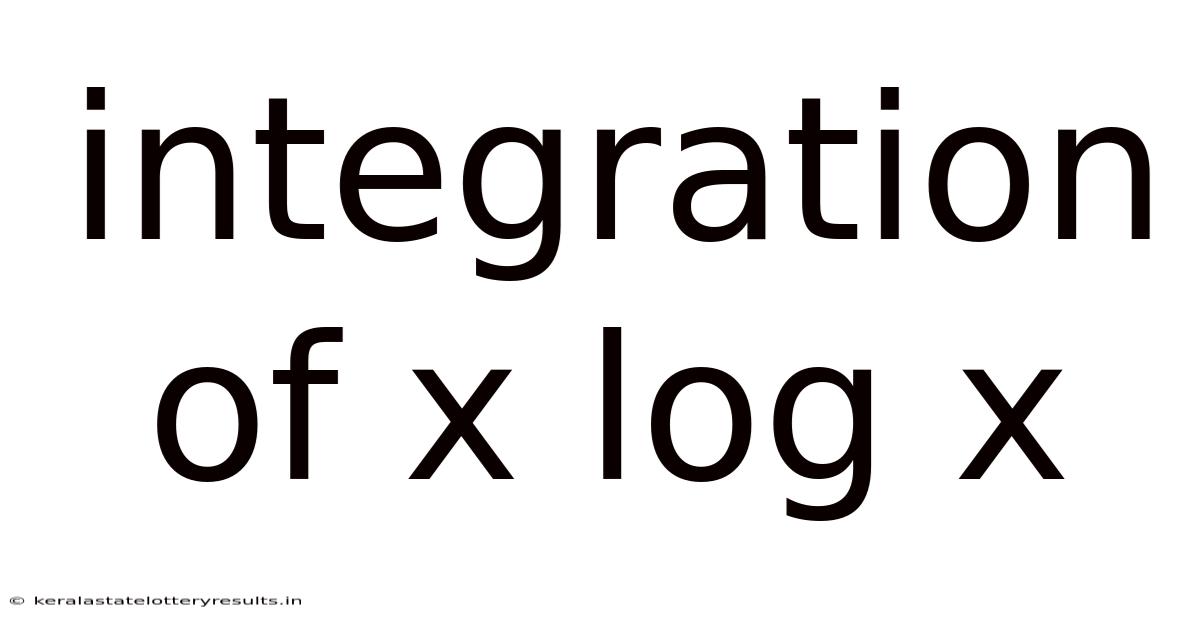
Table of Contents
The Integration of x ln x: A Comprehensive Guide
The integral of x ln x is a common problem encountered in calculus courses and various applications in science and engineering. Understanding its solution requires a grasp of integration by parts, a powerful technique for tackling integrals involving products of functions. This comprehensive guide will walk you through the process of integrating x ln x, exploring the underlying theory, providing a step-by-step solution, and addressing frequently asked questions. We will also delve into the broader context of this integral, highlighting its relevance in different fields.
Introduction: Understanding Integration by Parts
Before tackling the integral of x ln x, let's refresh our understanding of integration by parts. This technique stems from the product rule of differentiation: d(uv) = u dv + v du. Integrating both sides, we get:
∫d(uv) = ∫u dv + ∫v du
uv = ∫u dv + ∫v du
Rearranging this equation, we arrive at the formula for integration by parts:
∫u dv = uv - ∫v du
Choosing the appropriate 'u' and 'dv' is crucial for successful application of this method. A common mnemonic is "LIATE," prioritizing the order of functions for 'u': Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential.
Step-by-Step Solution: Integrating x ln x
Now, let's integrate x ln x. We'll use integration by parts:
-
Choosing u and dv: Following the LIATE rule, we choose:
- u = ln x => du = (1/x) dx
- dv = x dx => v = (1/2)x²
-
Applying the integration by parts formula:
∫x ln x dx = uv - ∫v du
Substituting our choices for u, v, and du:
∫x ln x dx = (1/2)x² ln x - ∫(1/2)x²(1/x) dx
-
Simplifying and Integrating:
∫x ln x dx = (1/2)x² ln x - ∫(1/2)x dx
The remaining integral is straightforward:
∫(1/2)x dx = (1/4)x² + C (where C is the constant of integration)
-
Final Result:
Therefore, the final result of integrating x ln x is:
∫x ln x dx = (1/2)x² ln x - (1/4)x² + C
The Scientific Explanation and Applications
The integral of x ln x, as we've seen, yields a relatively simple expression. However, the underlying mathematical concepts and its practical applications are far-reaching. Let's explore some of the scientific aspects and applications:
-
Probability and Statistics: This integral frequently appears in probability density functions (PDFs) and calculations involving expected values. For example, in certain continuous probability distributions, the expected value might require the evaluation of this specific integral. Understanding this integral is crucial for accurately calculating statistical parameters.
-
Information Theory: The concept of information entropy, a cornerstone of information theory, involves integrals similar to the one we've solved. This integral plays a role in quantifying uncertainty and information content within various systems.
-
Physics: In certain areas of physics, especially those involving logarithmic relationships, this integral can appear in calculations relating to energy, work, or other physical quantities.
-
Economics and Finance: Integrals involving logarithmic functions, particularly those resembling ∫x ln x dx, can emerge in economic models that deal with utility functions or cost-benefit analyses. These models often incorporate logarithmic scales to represent diminishing marginal utility or returns.
-
Numerical Integration Techniques: While we've solved the integral analytically, in many cases, integrals don't possess simple closed-form solutions. Numerical methods, such as the trapezoidal rule or Simpson's rule, can be employed to approximate the definite integral of x ln x over a specific interval. These techniques are valuable when dealing with complex functions or functions that lack elementary antiderivatives.
-
Differential Equations: The integral of x ln x can emerge as a part of the solution process for certain ordinary differential equations (ODEs). The appearance of logarithmic terms in ODEs is often related to phenomena exhibiting exponential growth or decay.
-
Computer Science: Algorithms that involve logarithmic complexity (e.g., binary search) can lead to integrals involving logarithmic functions during analysis of their time or space efficiency. Understanding such integrals is necessary for precise performance analysis.
Beyond the Basic Integral: Exploring Variations
The integral of x ln x serves as a foundational example. Let’s briefly explore some variations:
-
∫x² ln x dx: A similar approach using integration by parts, but with different choices for u and dv, will solve this integral. You'll choose u = ln x and dv = x² dx. The process is analogous to the one demonstrated earlier.
-
∫xⁿ ln x dx (where n is a constant): This generalization can also be solved using integration by parts repeatedly. The solution will involve powers of x and the logarithm.
-
∫ln x dx: This simpler integral, involving only the natural logarithm, can be solved using integration by parts by setting u = ln x and dv = dx. The solution is x ln x - x + C. This simpler integral is often a stepping stone to tackling more complex integrals involving logarithmic functions.
-
Definite Integrals: To evaluate a definite integral, such as ∫[a, b] x ln x dx, we simply evaluate the indefinite integral [(1/2)x² ln x - (1/4)x²] at the upper limit (b) and subtract its value at the lower limit (a). Remember to consider the appropriate limits of integration.
Frequently Asked Questions (FAQ)
Q1: Why is choosing 'u' and 'dv' important in integration by parts?
A1: The choice of 'u' and 'dv' significantly impacts the complexity of the integral after applying the integration by parts formula. A poor choice can lead to an even more complicated integral, while a good choice simplifies the subsequent integration steps. The LIATE rule provides a helpful guideline, but practice is crucial in developing intuition for making effective choices.
Q2: What if the integral is a definite integral?
A2: For a definite integral, you would follow the same integration by parts steps to find the indefinite integral and then evaluate it at the upper and lower limits of integration, subtracting the lower limit's value from the upper limit's value.
Q3: Are there other methods for solving this integral?
A3: While integration by parts is the most straightforward and commonly used method, more advanced techniques might be applicable in more complex scenarios. However, for the basic integral of x ln x, integration by parts is the most efficient and easily understandable approach.
Q4: What if the logarithm isn't the natural logarithm (ln x)?
A4: If you encounter a logarithm with a different base, you can convert it to the natural logarithm using the change of base formula: logₐ x = (ln x) / (ln a). Then, you can proceed with integration by parts.
Conclusion: Mastering the Integration of x ln x
The integral of x ln x, although seemingly simple at first glance, opens doors to a deeper understanding of integration techniques and their applications in various scientific and engineering disciplines. By mastering this integral and the integration by parts method, you gain valuable tools for tackling a wide range of calculus problems. Remember that practice is key to mastering integration. Work through various examples and variations to solidify your understanding and build your problem-solving skills. This integral serves as a stepping stone to more complex integrals and illustrates the elegance and power of calculus in solving real-world problems. The journey of learning calculus is a rewarding one, and mastering integrals like this one is a significant step toward mathematical fluency.
Latest Posts
Latest Posts
-
How Do You Spell 45
Sep 17, 2025
-
10 3 As A Fraction
Sep 17, 2025
-
What Is 34 Divisible By
Sep 17, 2025
-
180 Lbs Convert To Kg
Sep 17, 2025
-
How Many Mph Is 300kmh
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Integration Of X Log X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.