Integrate X 2 X 3
keralas
Sep 17, 2025 · 5 min read
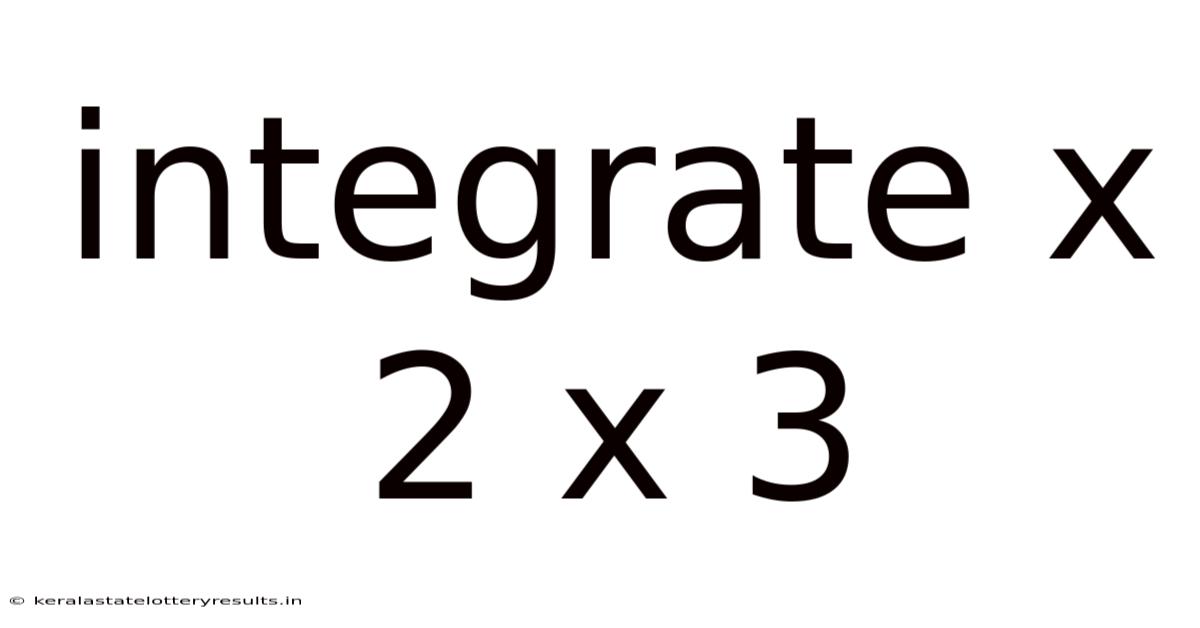
Table of Contents
Decoding the Mystery: A Deep Dive into Integrating x² * 3
This article will explore the intricacies of integrating the function x² * 3, providing a comprehensive understanding suitable for students from introductory calculus to those seeking a deeper grasp of integration techniques. We'll cover the fundamental steps, the underlying mathematical principles, and address common questions to ensure a thorough understanding of this seemingly simple, yet surprisingly illustrative, problem. This guide will equip you with the knowledge to tackle similar integration problems with confidence.
Introduction: Understanding Integration
Integration, a cornerstone of calculus, is essentially the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the area under the curve of a function. This area represents the accumulation of the function's value over a given interval. The integral of a function, often denoted by ∫f(x)dx, represents the antiderivative of that function. The "dx" signifies that we are integrating with respect to the variable x. Understanding this fundamental concept is crucial before tackling the integration of x² * 3.
Step-by-Step Integration of 3x²
The problem at hand is to integrate the function 3x². This is a relatively straightforward example, but understanding its solution provides a solid foundation for more complex integrations. Let's break down the process:
-
Apply the Power Rule of Integration: The power rule is a fundamental technique for integrating polynomial functions. It states that the integral of xⁿ is (xⁿ⁺¹)/(n+1) + C, where n is any real number except -1, and C is the constant of integration.
-
Applying the Rule to 3x²: In our case, we have 3x², which can be written as 3 * x². The constant 3 can be factored out of the integral because integration is a linear operator. Therefore, we have:
∫3x² dx = 3 ∫x² dx
-
Integrating x²: Now we apply the power rule to x². Here, n = 2. Therefore:
∫x² dx = (x²⁺¹)/(2+1) + C = x³/3 + C
-
Combining the Constant: Combining the constant 3, we get:
3 ∫x² dx = 3 * (x³/3 + C) = x³ + 3C
-
Simplifying the Constant of Integration: Since 3C is still an arbitrary constant, we can simply rewrite it as C. Therefore, the final result is:
∫3x² dx = x³ + C
The Significance of the Constant of Integration (C)
The constant of integration, C, is a crucial element in indefinite integration. It represents a family of functions, all differing only by a constant, which have the same derivative. This is because the derivative of a constant is always zero. Therefore, when finding the antiderivative, we must always include the constant C to account for all possible functions that could have produced the original function.
Explanation of the Mathematical Principles
The integration of 3x² relies on several core mathematical concepts:
-
Linearity of Integration: This property allows us to treat the integral of a sum or difference of functions as the sum or difference of their individual integrals. It also permits factoring out constants, as demonstrated in step 2.
-
The Fundamental Theorem of Calculus: This theorem establishes the link between differentiation and integration, stating that integration is the reverse process of differentiation. It underpins the entire process of finding antiderivatives.
-
The Power Rule: As mentioned earlier, the power rule is a specific application of the fundamental theorem of calculus for polynomial functions. It is a fundamental tool in evaluating a wide range of integrals.
Definite Integration: Applying Limits
The integration we performed above is indefinite integration, meaning it doesn't have specific limits of integration. If we were to perform definite integration, we would specify the interval over which we want to find the area under the curve. This would involve evaluating the antiderivative at the upper and lower limits and then subtracting the two values. For example, to find the definite integral of 3x² from x = 1 to x = 2, we would do the following:
- Evaluate x³ at x = 2: 2³ = 8
- Evaluate x³ at x = 1: 1³ = 1
- Subtract the lower limit from the upper limit: 8 - 1 = 7
Therefore, the definite integral of 3x² from 1 to 2 is 7. This represents the area under the curve of 3x² between x = 1 and x = 2.
Practical Applications
The seemingly simple integration of 3x² has numerous real-world applications:
-
Physics: Calculating displacement from acceleration (where acceleration is represented by a function similar to 3x²).
-
Engineering: Determining the volume of solids of revolution.
-
Economics: Finding total cost from marginal cost (where marginal cost is represented by a function similar to 3x²).
-
Statistics: Calculating probabilities using continuous probability distributions.
Frequently Asked Questions (FAQ)
-
Q: What happens if I forget the constant of integration (C)?
A: While it might seem insignificant, omitting C is a significant error. It means you are only considering one specific function from a family of functions that share the same derivative. In definite integration, the constant cancels out, but it is still crucial to include it in indefinite integration.
-
Q: Can I use other integration techniques besides the power rule for 3x²?
A: For this specific function, the power rule is the most efficient method. However, other techniques like integration by substitution or integration by parts become necessary for more complex functions.
-
Q: What if the function was more complex, like 3x² + 2x + 1?
A: The linearity of integration allows us to integrate each term separately. So:
∫(3x² + 2x + 1)dx = ∫3x² dx + ∫2x dx + ∫1 dx = x³ + x² + x + C
-
Q: How do I check if my integration is correct?
A: Differentiate your answer. If you get back the original function, your integration was correct. For example, differentiating x³ + C gives 3x², which is our original function.
Conclusion: Mastering the Fundamentals
Integrating 3x² might seem elementary, but mastering its integration provides a crucial foundation for more advanced calculus concepts. Understanding the power rule, the importance of the constant of integration, and the underlying principles discussed in this article will equip you to tackle more complex integration problems with greater confidence and accuracy. Remember, consistent practice and a solid understanding of the fundamental principles are key to success in calculus and its numerous applications. The seemingly simple act of integrating 3x² serves as a gateway to a vast and powerful mathematical world.
Latest Posts
Latest Posts
-
How To Do Linear Approximation
Sep 17, 2025
-
What Equals 75 In Multiplication
Sep 17, 2025
-
Lcm Of 12 And 28
Sep 17, 2025
-
How Long Is 7 Months
Sep 17, 2025
-
2 Million How Many Zeros
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Integrate X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.