Hcf Of 15 And 18
keralas
Sep 13, 2025 · 5 min read
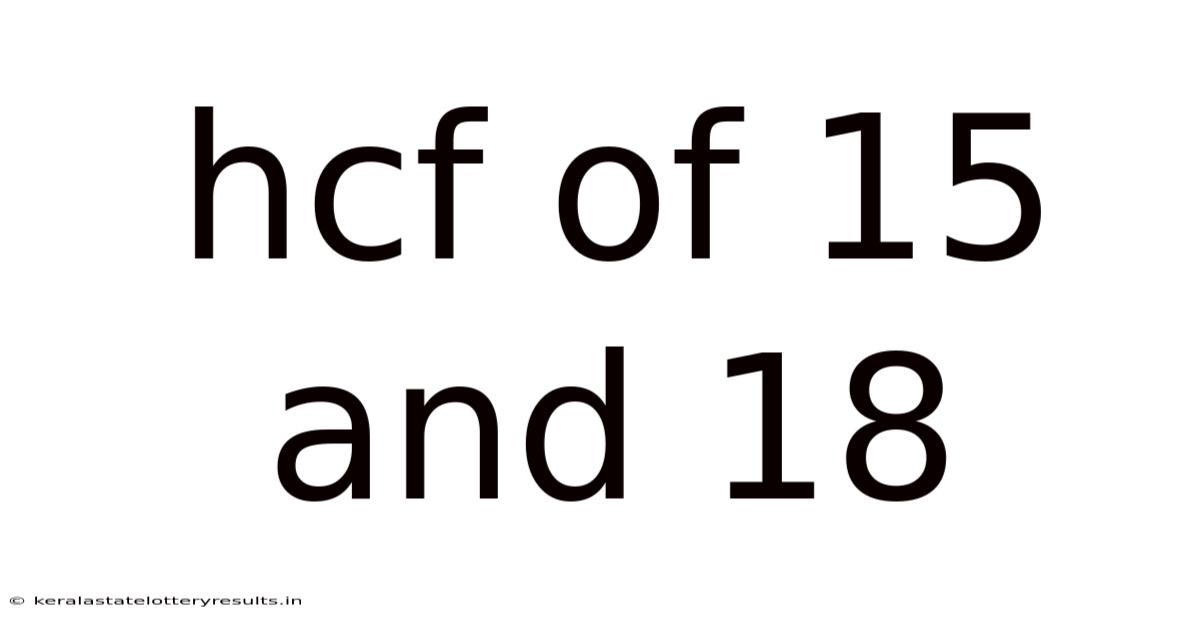
Table of Contents
Finding the Highest Common Factor (HCF) of 15 and 18: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve into the process of determining the HCF of 15 and 18, exploring various methods and providing a deep understanding of the underlying principles. We'll move beyond simply stating the answer and explore the "why" behind the calculations, making this a valuable resource for students and anyone looking to refresh their understanding of number theory.
Introduction to Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It represents the greatest common divisor shared by the numbers. Understanding HCF is crucial for simplifying fractions, solving problems in algebra, and many other mathematical applications. In this article, we will focus on finding the HCF of 15 and 18, using several different approaches.
Method 1: Prime Factorization
This is a highly effective method for finding the HCF of any two numbers, especially larger ones. The process involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 15 and 18:
- 15: 15 can be expressed as 3 x 5. Both 3 and 5 are prime numbers.
- 18: 18 can be expressed as 2 x 3 x 3 or 2 x 3². 2 and 3 are prime numbers.
Now, we identify the common prime factors: Both 15 and 18 share a common prime factor of 3.
To find the HCF, we multiply the common prime factors: In this case, the only common prime factor is 3. Therefore, the HCF of 15 and 18 is 3.
Method 2: Listing Factors
This method is suitable for smaller numbers and involves listing all the factors of each number and then identifying the largest common factor.
Factors of 15: 1, 3, 5, 15 Factors of 18: 1, 2, 3, 6, 9, 18
By comparing the two lists, we can see that the common factors are 1 and 3. The largest of these common factors is 3. Therefore, the HCF of 15 and 18 is 3.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the HCF, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the HCF.
Let's apply the Euclidean Algorithm to 15 and 18:
- Divide the larger number (18) by the smaller number (15): 18 ÷ 15 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (3): 15 ÷ 3 = 5 with a remainder of 0.
- Since the remainder is 0, the last non-zero remainder (3) is the HCF.
Therefore, the HCF of 15 and 18 is 3.
Understanding the Concept of Divisibility
The HCF is intrinsically linked to the concept of divisibility. A number 'a' is said to be divisible by a number 'b' if the division of 'a' by 'b' leaves no remainder (i.e., the remainder is 0). The HCF represents the largest number that divides both numbers without leaving a remainder. In the case of 15 and 18, 3 is the largest number that perfectly divides both.
Applications of HCF
The HCF has numerous applications in various areas of mathematics and beyond. Here are some examples:
-
Simplifying Fractions: The HCF is used to simplify fractions to their lowest terms. For example, the fraction 15/18 can be simplified by dividing both the numerator and denominator by their HCF (3), resulting in the simplified fraction 5/6.
-
Solving Word Problems: Many word problems involving quantities that need to be divided equally rely on finding the HCF. For example, if you have 15 apples and 18 oranges, and you want to divide them into equal groups, the HCF (3) tells you that you can create 3 equal groups.
-
Number Theory: HCF plays a critical role in number theory, particularly in topics such as modular arithmetic and cryptography.
-
Geometry: The HCF can be used in geometry problems related to finding the dimensions of objects that can be divided into equal parts.
Frequently Asked Questions (FAQ)
Q: What is the difference between HCF and LCM?
A: The Highest Common Factor (HCF) is the largest number that divides both numbers without leaving a remainder. The Least Common Multiple (LCM) is the smallest number that is a multiple of both numbers. While HCF identifies the common divisors, LCM identifies the common multiples. For 15 and 18, the HCF is 3, and the LCM is 90. There's a relationship between HCF and LCM: HCF(a, b) x LCM(a, b) = a x b.
Q: Can the HCF of two numbers be 1?
A: Yes. If two numbers have no common factors other than 1, their HCF is 1. Such numbers are called relatively prime or coprime. For example, the HCF of 15 and 8 is 1.
Q: Is there a limit to the size of numbers for which we can find the HCF?
A: No. Methods like the Euclidean Algorithm are efficient even for very large numbers, making it possible to find the HCF of practically any two integers.
Q: Are there other methods to find the HCF besides those mentioned?
A: Yes, there are more advanced algorithms and techniques, especially for finding the HCF of more than two numbers or very large numbers. However, the methods discussed here are sufficient for most practical purposes.
Conclusion
Finding the Highest Common Factor (HCF) is a fundamental skill in mathematics with wide-ranging applications. We've explored three effective methods – prime factorization, listing factors, and the Euclidean Algorithm – for determining the HCF of 15 and 18, concluding that the HCF is 3. Understanding the concept of divisibility and the various applications of HCF will not only improve your mathematical skills but also provide a solid foundation for more advanced mathematical concepts. Remember that choosing the most efficient method depends on the size and complexity of the numbers involved. For smaller numbers, listing factors or prime factorization may be sufficient, while the Euclidean Algorithm is more efficient for larger numbers.
Latest Posts
Latest Posts
-
Interior Angles In A Nonagon
Sep 13, 2025
-
Symmetry Lines Of A Circle
Sep 13, 2025
-
1 16 In Decimal Form
Sep 13, 2025
-
Net For Right Triangular Prism
Sep 13, 2025
-
Is 38 Prime Or Composite
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 15 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.