Gcf Of 8 And 14
keralas
Sep 13, 2025 · 6 min read
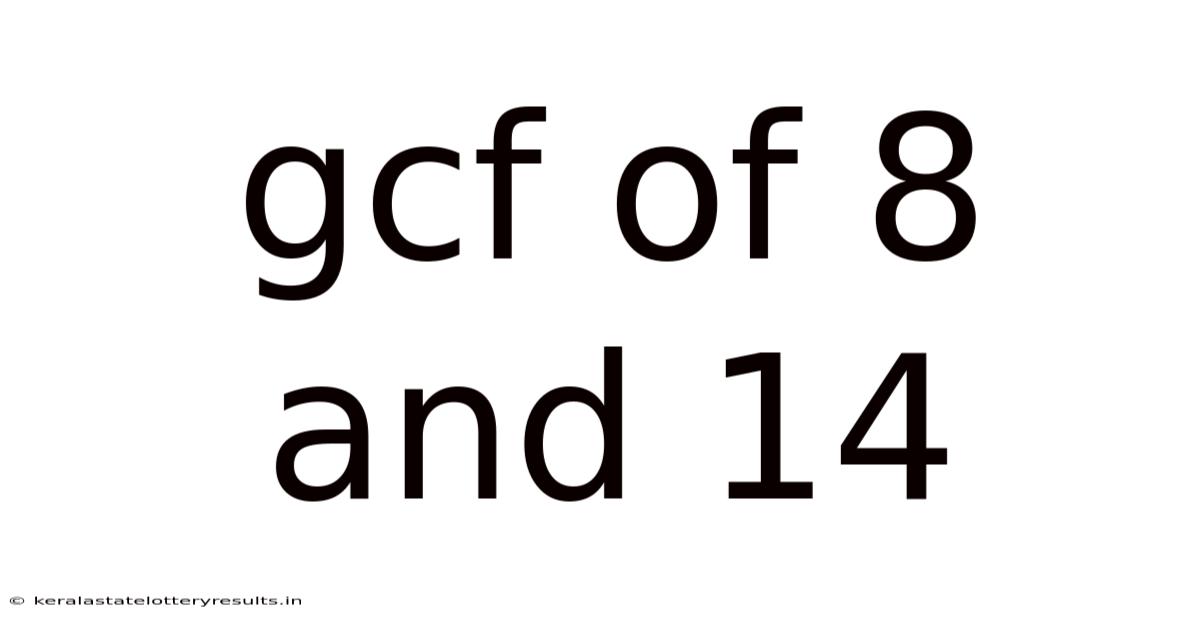
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 8 and 14: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for calculating the GCF opens doors to a richer understanding of number theory and its applications in mathematics and computer science. This article will explore the GCF of 8 and 14 in detail, examining different approaches and providing a comprehensive explanation of the concepts involved. We'll go beyond a simple answer, delving into the theoretical foundation and practical applications of finding the greatest common factor.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly.
Understanding the concept of factors is crucial. Factors are numbers that divide another number without leaving a remainder. For example, the factors of 8 are 1, 2, 4, and 8. The factors of 14 are 1, 2, 7, and 14. The GCF is the largest number that appears in both lists of factors.
Method 1: Listing Factors
The most straightforward method for finding the GCF of relatively small numbers like 8 and 14 is to list all the factors of each number and identify the largest common factor.
Factors of 8: 1, 2, 4, 8 Factors of 14: 1, 2, 7, 14
Comparing the two lists, we see that the common factors are 1 and 2. The largest of these common factors is 2. Therefore, the GCF of 8 and 14 is 2.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the GCF of larger numbers. It involves expressing each number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 8 and 14:
- 8 = 2 x 2 x 2 = 2³ (8 is a composite number, meaning it is not prime, and can be written as a product of primes)
- 14 = 2 x 7
Now, we identify the common prime factors. Both 8 and 14 share one factor of 2. The GCF is the product of the common prime factors raised to the lowest power. In this case, the lowest power of 2 is 2¹, so the GCF of 8 and 14 is 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two integers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 8 and 14:
- 14 = 8 x 1 + 6 (We divide 14 by 8, the quotient is 1, and the remainder is 6)
- 8 = 6 x 1 + 2 (We divide 8 by 6, the quotient is 1, and the remainder is 2)
- 6 = 2 x 3 + 0 (We divide 6 by 2, the quotient is 3, and the remainder is 0)
When the remainder becomes 0, the GCF is the last non-zero remainder, which is 2. The Euclidean algorithm provides a systematic and efficient approach, especially useful for larger numbers where listing factors becomes cumbersome.
Visualizing the GCF with Venn Diagrams
Venn diagrams can provide a visual representation of the factors and the GCF. We can represent the factors of 8 and 14 in separate circles, with overlapping sections representing common factors.
[Imagine a Venn diagram here. One circle labeled "Factors of 8" containing 1, 2, 4, 8. Another circle labeled "Factors of 14" containing 1, 2, 7, 14. The overlapping section contains 1 and 2.]
The overlapping section shows the common factors. The largest number in the overlapping section, 2, represents the GCF.
Applications of Finding the GCF
Finding the GCF has numerous practical applications in various areas:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 8/14 can be simplified by dividing both the numerator and denominator by their GCF, which is 2, resulting in the simplified fraction 4/7.
-
Solving Word Problems: Many word problems involve finding the GCF to determine the largest possible size of groups or the maximum number of items that can be equally distributed.
-
Cryptography: The GCF plays a significant role in cryptographic algorithms, particularly in RSA encryption, where finding the GCF of two large numbers is essential.
-
Computer Science: The Euclidean algorithm, used for finding the GCF, is a fundamental algorithm in computer science with applications in various areas like computer graphics and data compression.
Beyond the Basics: Least Common Multiple (LCM)
While we've focused on the GCF, it's important to understand its relationship with the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related by the following formula:
GCF(a, b) x LCM(a, b) = a x b
For 8 and 14:
GCF(8, 14) = 2 LCM(8, 14) = 56
2 x 56 = 112 and 8 x 14 = 112. The formula holds true.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can the GCF of two numbers be greater than either of the numbers?
- A: No. The GCF is always less than or equal to the smaller of the two numbers.
-
Q: How do I find the GCF of more than two numbers?
- A: You can extend the methods discussed above. For prime factorization, find the prime factorization of each number and identify the common prime factors raised to the lowest power. For the Euclidean algorithm, you can find the GCF of two numbers, and then find the GCF of that result and the next number, and so on.
Conclusion
Finding the greatest common factor of 8 and 14, which is 2, is a seemingly simple task, but it serves as a gateway to understanding fundamental concepts in number theory. Through various methods—listing factors, prime factorization, and the Euclidean algorithm—we've explored different approaches to arrive at the same answer. The GCF has widespread applications beyond basic arithmetic, extending into areas like fraction simplification, cryptography, and computer science. By understanding the GCF and its related concepts, we gain a deeper appreciation for the elegance and power of mathematical principles. This foundational knowledge forms the basis for more advanced mathematical concepts and problem-solving strategies. Further exploration into number theory will reveal even more fascinating applications and connections to other branches of mathematics.
Latest Posts
Latest Posts
-
How Long Is 24 Weeks
Sep 13, 2025
-
Pi Is A Rational Number
Sep 13, 2025
-
7 And 9 Common Denominator
Sep 13, 2025
-
Diagonal Of A Rectangular Prism
Sep 13, 2025
-
What Is Standard Polynomial Form
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 8 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.