Gcf Of 27 And 6
keralas
Sep 17, 2025 · 6 min read
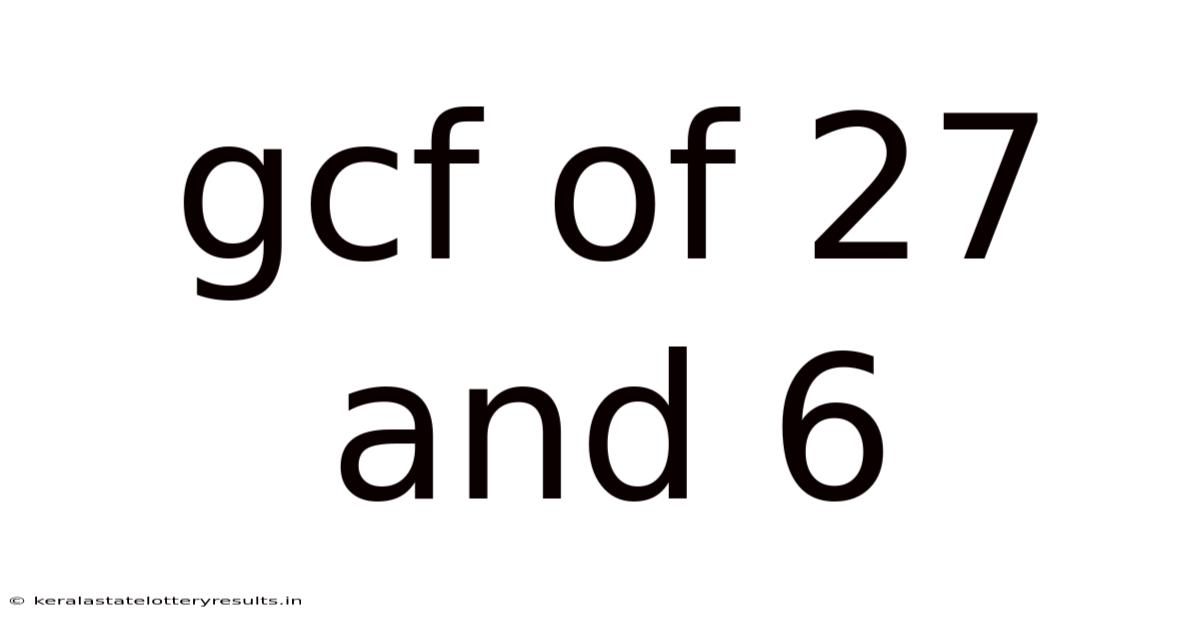
Table of Contents
Understanding the Greatest Common Factor (GCF) of 27 and 6: A Comprehensive Guide
Finding the greatest common factor (GCF) of two numbers, like 27 and 6, might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the GCF is crucial for grasping more advanced mathematical concepts later on. This comprehensive guide will delve into the GCF of 27 and 6, explaining various approaches, their applications, and the broader mathematical principles involved. We'll explore everything from basic methods suitable for elementary school students to more sophisticated techniques used in higher mathematics.
Introduction to the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. Understanding GCFs is fundamental in simplifying fractions, solving algebraic equations, and even in more advanced areas like number theory and cryptography.
This article will specifically address the GCF of 27 and 6, providing a step-by-step walkthrough of various methods to calculate it, and exploring the reasons behind the process. We'll also touch upon some real-world applications of GCFs to show their practical significance.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers like 27 and 6, is listing all the factors of each number and then identifying the largest common factor.
Factors of 27: 1, 3, 9, 27
Factors of 6: 1, 2, 3, 6
By comparing the two lists, we can see that the common factors are 1 and 3. The largest of these common factors is 3. Therefore, the GCF of 27 and 6 is 3.
This method works well for smaller numbers but becomes less efficient as the numbers get larger. Imagine trying to list all factors of a large number like 1575!
Method 2: Prime Factorization
Prime factorization is a more systematic and efficient method for finding the GCF, especially for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 27 and 6:
- Prime factorization of 27: 3 x 3 x 3 = 3³
- Prime factorization of 6: 2 x 3
Now, identify the common prime factors. Both numbers have at least one factor of 3. We select the lowest power of the common prime factor, which is 3¹. Therefore, the GCF of 27 and 6 is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, regardless of their size. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 27 and 6:
- Step 1: Subtract the smaller number (6) from the larger number (27): 27 - 6 = 21
- Step 2: Now find the GCF of 21 and 6. Repeat the subtraction: 21 - 6 = 15
- Step 3: Find the GCF of 15 and 6: 15 - 6 = 9
- Step 4: Find the GCF of 9 and 6: 9 - 6 = 3
- Step 5: Find the GCF of 6 and 3: 6 - 3 = 3
- Step 6: Find the GCF of 3 and 3. Since both numbers are the same, the GCF is 3.
Therefore, the GCF of 27 and 6 is 3. The Euclidean algorithm is particularly powerful for larger numbers because it avoids the need to find all factors.
Understanding the Importance of the GCF
The GCF isn't just a mathematical curiosity; it has numerous applications across various fields:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 27/6 can be simplified by dividing both the numerator and the denominator by their GCF (3), resulting in the simplified fraction 9/2.
-
Solving Algebraic Equations: The GCF plays a crucial role in factoring algebraic expressions. Finding the GCF of the terms allows for simplification and easier solving of equations.
-
Geometry and Measurement: The GCF is used in problems involving area and perimeter calculations where we need to find the largest common divisor of lengths or dimensions. For example, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the floor's dimensions.
-
Number Theory and Cryptography: The concept of GCF forms the basis of many advanced mathematical concepts in number theory and cryptography, including the RSA algorithm, which is widely used for secure data encryption.
Frequently Asked Questions (FAQs)
-
What if the GCF of two numbers is 1? If the GCF of two numbers is 1, they are considered relatively prime or coprime. This means they share no common factors other than 1.
-
Can the GCF of two numbers be larger than either of the numbers? No, the GCF can never be larger than the smaller of the two numbers.
-
Is there a GCF for more than two numbers? Yes, the concept of GCF extends to more than two numbers. To find the GCF of multiple numbers, you can use prime factorization or the Euclidean algorithm (with modifications). For example, to find the GCF of 27, 6, and 18, you would find the prime factorization of each number and choose the common prime factors with their lowest power.
-
Are there any online calculators or tools to find the GCF? Yes, many online calculators are available that can efficiently compute the GCF of two or more numbers. These calculators can be especially helpful for dealing with large numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor (GCF) of two numbers, such as 27 and 6, is a fundamental skill in mathematics with wide-ranging applications. We've explored three different methods—listing factors, prime factorization, and the Euclidean algorithm—each with its strengths and weaknesses. Understanding these methods provides a strong foundation for tackling more complex mathematical problems. Remember that mastering the GCF is not just about calculating a single value; it’s about comprehending the underlying principles of number theory and appreciating its practical relevance in various fields. From simplifying fractions to solving advanced equations, the GCF plays a vital role, highlighting the importance of understanding its calculation and applications. This knowledge will serve you well in your continued mathematical journey, enabling you to tackle progressively challenging concepts with confidence.
Latest Posts
Latest Posts
-
One Thousand One Hundred Fifty
Sep 17, 2025
-
8 Is Prime Or Composite
Sep 17, 2025
-
Gcf Of 51 And 34
Sep 17, 2025
-
Is 28 Composite Or Prime
Sep 17, 2025
-
What Equals 19 In Multiplication
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 27 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.