Gcf Of 21 And 28
keralas
Sep 17, 2025 · 6 min read
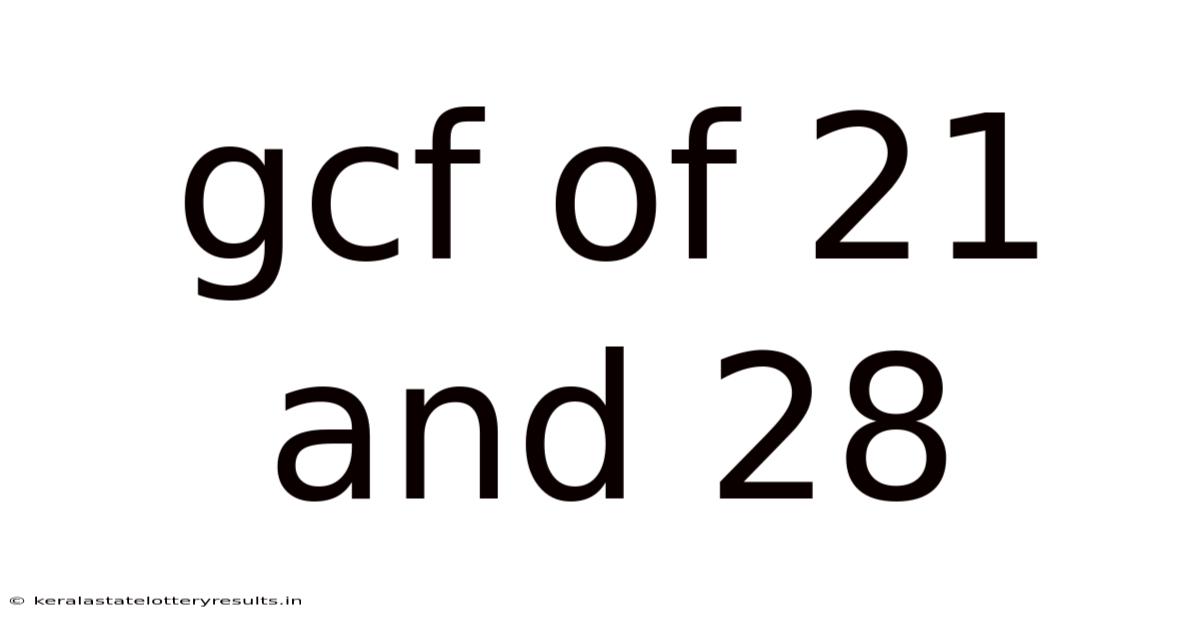
Table of Contents
Finding the Greatest Common Factor (GCF) of 21 and 28: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This guide will explore multiple methods for determining the GCF of 21 and 28, providing a detailed explanation suitable for learners of all levels. We'll delve into the underlying principles, illustrate different techniques, and address frequently asked questions, ensuring a thorough understanding of this important mathematical operation.
Understanding Greatest Common Factor (GCF)
The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding the GCF is crucial for various mathematical applications, including simplifying fractions, solving algebraic equations, and working with geometric problems. This article will specifically focus on finding the GCF of 21 and 28, showcasing various approaches.
Method 1: Listing Factors
This method is straightforward and ideal for beginners. We begin by listing all the factors of each number. Factors are numbers that divide evenly into a given number.
- Factors of 21: 1, 3, 7, 21
- Factors of 28: 1, 2, 4, 7, 14, 28
Now, we compare the two lists and identify the common factors: 1 and 7. The greatest of these common factors is 7. Therefore, the GCF of 21 and 28 is 7.
Method 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). This method is more efficient for larger numbers.
-
Prime Factorization of 21: 21 = 3 x 7
-
Prime Factorization of 28: 28 = 2 x 2 x 7 = 2² x 7
-
Identifying Common Prime Factors: Both 21 and 28 share the prime factor 7.
-
Calculating the GCF: To find the GCF, we multiply the common prime factors together. In this case, the only common prime factor is 7. Therefore, the GCF of 21 and 28 is 7.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. We repeat this process until we reach a point where the difference is zero. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 21 and 28:
-
Step 1: Subtract the smaller number (21) from the larger number (28): 28 - 21 = 7
-
Step 2: Since the remainder (7) is not zero, we replace the larger number (28) with the remainder (7) and repeat the process using 21 and 7: 21 - (2 x 7) = 7
-
Step 3: Repeat the process: 7 - 7 = 0
Since the remainder is now 0, the last non-zero remainder (7) is the GCF. Therefore, the GCF of 21 and 28 is 7.
Method 4: Venn Diagram
A Venn diagram provides a visual representation of the common factors. We can represent the factors of 21 and 28 in separate circles, with the overlapping section representing the common factors.
[Imagine a Venn Diagram here: Circle 1: Factors of 21 (1, 3, 7, 21); Circle 2: Factors of 28 (1, 2, 4, 7, 14, 28); Overlapping section: 1, 7]
The common factors are 1 and 7. The greatest common factor is therefore 7.
Understanding the Significance of GCF
The GCF has many practical applications:
-
Simplifying Fractions: To simplify a fraction, we divide both the numerator and denominator by their GCF. For example, the fraction 21/28 can be simplified to 3/4 by dividing both the numerator and denominator by their GCF, 7.
-
Solving Algebraic Equations: The GCF plays a role in factoring algebraic expressions, simplifying equations, and finding solutions.
-
Geometric Problems: The GCF is used in geometric problems involving area, volume, and other related calculations. For instance, finding the side length of the largest possible square tiles that can be used to cover a rectangular floor with dimensions 21 units and 28 units would involve determining the GCF.
-
Number Theory: GCF is a fundamental concept in number theory, which is a branch of mathematics dealing with the properties of numbers.
Further Exploration and Related Concepts
Understanding the GCF leads to a deeper understanding of other related mathematical concepts, including:
-
Least Common Multiple (LCM): The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. The relationship between GCF and LCM is given by the formula: GCF(a, b) x LCM(a, b) = a x b. For 21 and 28, the LCM is 84.
-
Divisibility Rules: Knowing divisibility rules for different numbers (e.g., a number is divisible by 3 if the sum of its digits is divisible by 3) can help in identifying factors more quickly.
-
Modular Arithmetic: The GCF is important in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus).
Frequently Asked Questions (FAQ)
-
Q: Why is the GCF important?
- A: The GCF is crucial for simplifying expressions, solving equations, and understanding the relationships between numbers. It's a fundamental building block in many mathematical areas.
-
Q: Is there only one GCF for two numbers?
- A: Yes, there is only one greatest common factor for any pair of numbers.
-
Q: Can the GCF be 1?
- A: Yes, if two numbers are relatively prime (meaning they have no common factors other than 1), their GCF is 1.
-
Q: How do I choose the best method for finding the GCF?
- A: For small numbers, the listing factors method is easiest. For larger numbers, the Euclidean algorithm or prime factorization are more efficient.
-
Q: What if I have more than two numbers?
- A: You can extend these methods to find the GCF of more than two numbers. For example, you can find the GCF of 21, 28, and another number by first finding the GCF of 21 and 28, and then finding the GCF of that result and the third number.
Conclusion
Finding the greatest common factor (GCF) of 21 and 28, which is 7, can be achieved through various methods – listing factors, prime factorization, the Euclidean algorithm, or using a Venn diagram. Each method offers a unique approach, and the choice of method depends on the complexity of the numbers involved and the learner's comfort level. Understanding the GCF is fundamental to various mathematical concepts and has widespread applications across different fields. By mastering these different techniques, you'll build a strong foundation in number theory and related mathematical areas. Remember to practice regularly to solidify your understanding and become proficient in finding the GCF of any pair of numbers.
Latest Posts
Latest Posts
-
X 3 X 4 8
Sep 17, 2025
-
How Much Is 63 Inches
Sep 17, 2025
-
The Square Root Of 45
Sep 17, 2025
-
Pic Of 90 Degree Angle
Sep 17, 2025
-
How Do You Spell 45
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 21 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.