Gcf For 8 And 20
keralas
Sep 16, 2025 · 6 min read
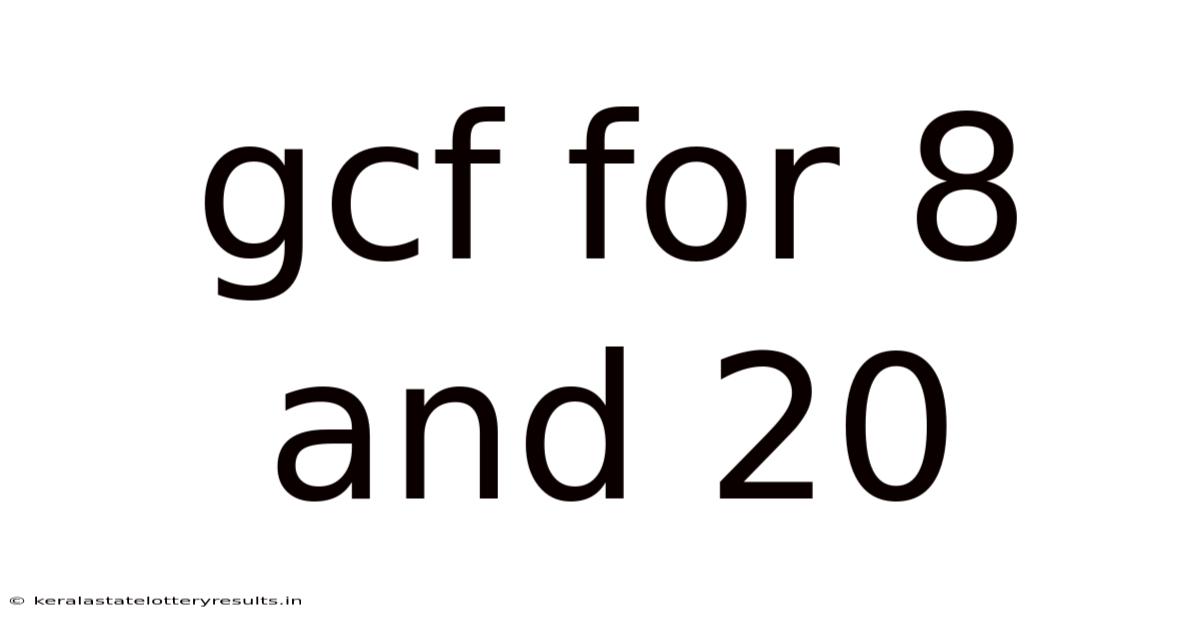
Table of Contents
Understanding the Greatest Common Factor (GCF) of 8 and 20: A Comprehensive Guide
Finding the greatest common factor (GCF) of two numbers, like 8 and 20, might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the GCF provides a valuable foundation for more advanced mathematical concepts. This comprehensive guide will not only show you how to find the GCF of 8 and 20 but will also delve into the theoretical underpinnings, explore multiple methods, and address frequently asked questions. By the end, you’ll have a solid grasp of GCF and its applications.
Introduction to the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding the GCF is crucial in various mathematical operations, including simplification of fractions and algebraic expressions.
Finding the GCF of 8 and 20: Methods and Explanations
There are several ways to determine the GCF of 8 and 20. Let's explore the most common methods:
1. Listing Factors Method
This is a straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest common factor.
- Factors of 8: 1, 2, 4, 8
- Factors of 20: 1, 2, 4, 5, 10, 20
Comparing the two lists, we see that the common factors are 1, 2, and 4. The greatest among these is 4. Therefore, the GCF of 8 and 20 is 4.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 20: 2 x 2 x 5 = 2² x 5
To find the GCF, we identify the common prime factors and their lowest powers. Both 8 and 20 share two factors of 2 (2²). Therefore, the GCF is 2 x 2 = 4.
3. Euclidean Algorithm
The Euclidean algorithm is a more efficient method for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until we reach a point where the remainder is 0. The last non-zero remainder is the GCF.
Let's apply it to 8 and 20:
- 20 = 8 x 2 + 4 (We divide 20 by 8. The quotient is 2 and the remainder is 4)
- 8 = 4 x 2 + 0 (We divide 8 by 4. The quotient is 2 and the remainder is 0)
Since the remainder is 0, the GCF is the last non-zero remainder, which is 4.
Understanding the Significance of the GCF
The GCF is not just a mathematical curiosity; it has several practical applications:
-
Simplifying Fractions: The GCF helps in simplifying fractions to their lowest terms. For example, the fraction 20/8 can be simplified by dividing both the numerator and the denominator by their GCF, which is 4. This simplifies the fraction to 5/2.
-
Solving Problems Involving Divisibility: The GCF is useful in determining whether a number is divisible by another number. If the GCF of two numbers is greater than 1, then they share common factors and are divisible by at least that GCF.
-
Geometry and Measurement: The GCF can be applied in geometry problems involving finding the dimensions of squares or rectangles that can be formed from a given area or perimeter.
-
Algebra and Number Theory: The GCF plays a vital role in more advanced mathematical concepts such as modular arithmetic, abstract algebra, and cryptography.
Beyond 8 and 20: Applying the Methods to Other Numbers
The methods explained above – listing factors, prime factorization, and the Euclidean algorithm – are applicable to finding the GCF of any two (or more) integers. Let's consider an example with larger numbers: finding the GCF of 48 and 72.
1. Listing Factors (Less Efficient for Larger Numbers):
Listing all the factors of 48 and 72 would be time-consuming. This method becomes less practical for larger numbers.
2. Prime Factorization:
- Prime factorization of 48: 2 x 2 x 2 x 2 x 3 = 2⁴ x 3
- Prime factorization of 72: 2 x 2 x 2 x 3 x 3 = 2³ x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2³ and the lowest power of 3 is 3¹. Therefore, the GCF of 48 and 72 is 2³ x 3 = 8 x 3 = 24.
3. Euclidean Algorithm:
- 72 = 48 x 1 + 24
- 48 = 24 x 2 + 0
The GCF is the last non-zero remainder, which is 24.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, they are said to be relatively prime or coprime. This means they share no common factors other than 1. For example, the GCF of 9 and 10 is 1.
Q2: Can we find the GCF of more than two numbers?
A2: Yes, we can extend the methods to find the GCF of more than two numbers. For the prime factorization method, we find the prime factorization of each number and identify the common prime factors with their lowest powers. For the Euclidean algorithm, we can find the GCF of two numbers, and then find the GCF of the result and the third number, and so on.
Q3: Is there a formula for calculating the GCF?
A3: There isn't a single, universally applicable formula for calculating the GCF. However, the methods described above (prime factorization and Euclidean algorithm) provide systematic ways to compute it.
Q4: How does the GCF relate to the Least Common Multiple (LCM)?
A4: The GCF and LCM are closely related. For any two numbers a and b, the product of their GCF and LCM is equal to the product of the two numbers: GCF(a, b) x LCM(a, b) = a x b. This relationship is useful in various mathematical applications.
Q5: What are some real-world applications of the GCF beyond what was mentioned earlier?
A5: The GCF finds applications in tasks such as dividing items into equally sized groups (e.g., sharing candies among friends), arranging objects in a grid pattern, and simplifying ratios and proportions. It also underpins many computer algorithms for tasks like data compression and encryption.
Conclusion
Finding the greatest common factor of two numbers, such as 8 and 20, is a fundamental skill in mathematics with diverse applications. While seemingly simple, understanding the underlying concepts and various methods—listing factors, prime factorization, and the Euclidean algorithm—provides a deeper appreciation of number theory and its practical relevance. This knowledge extends beyond basic arithmetic, forming a crucial foundation for advanced mathematical concepts and problem-solving in various fields. Mastering the GCF unlocks a deeper understanding of the relationships between numbers and paves the way for more complex mathematical explorations.
Latest Posts
Latest Posts
-
How To Find Factored Form
Sep 16, 2025
-
All The Factors Of 72
Sep 16, 2025
-
How To Integrate 2 X
Sep 16, 2025
-
How Long Is 1 M
Sep 16, 2025
-
Factors Of 20 And 24
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Gcf For 8 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.