55 Percent As A Fraction
keralas
Sep 16, 2025 · 5 min read
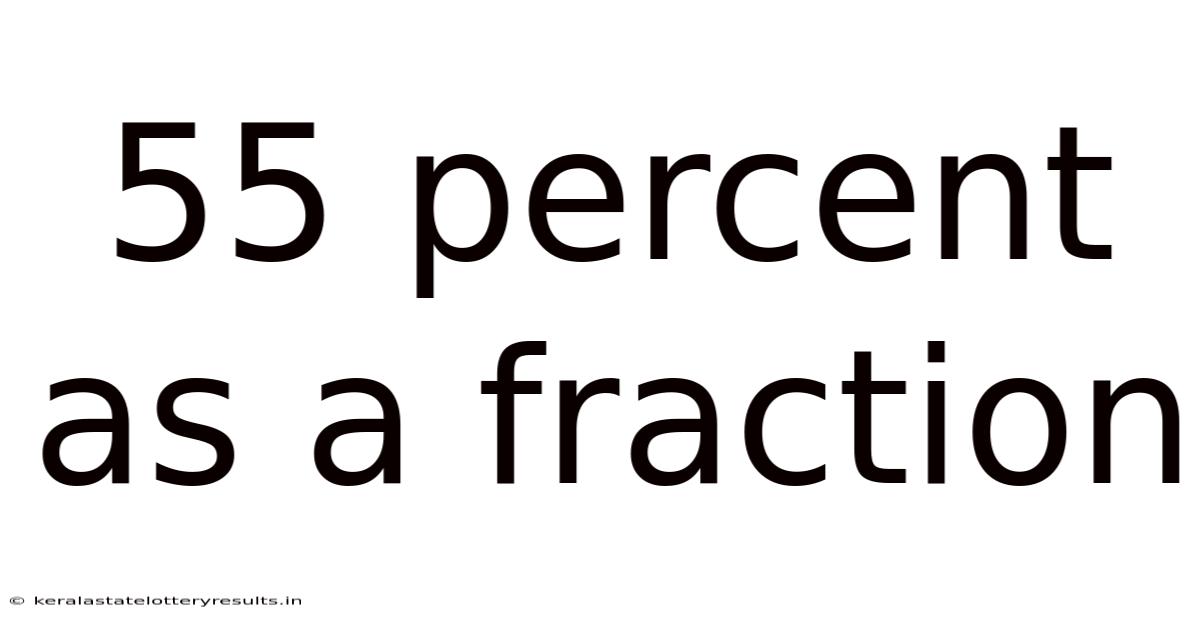
Table of Contents
55 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This comprehensive guide delves into the conversion of 55 percent to its fractional form, exploring the process, its simplified version, and related concepts. We'll also examine practical applications and answer frequently asked questions to solidify your understanding.
Introduction: Understanding Percentages and Fractions
Before we dive into the specifics of converting 55%, let's establish a clear understanding of percentages and fractions. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 55% means 55 out of 100.
A fraction, on the other hand, represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, ½ represents one part out of two equal parts. Converting a percentage to a fraction involves expressing the percentage as a fraction with a denominator of 100 and then simplifying it to its lowest terms.
Converting 55% to a Fraction: A Step-by-Step Guide
The conversion of 55% to a fraction is a straightforward process. Here's a step-by-step guide:
-
Write the percentage as a fraction with a denominator of 100: 55% can be written as 55/100. This directly reflects the definition of percentage – 55 parts out of 100.
-
Simplify the fraction: The fraction 55/100 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (55) and the denominator (100). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD of 55 and 100 is 5.
-
Divide both the numerator and the denominator by the GCD: Dividing both 55 and 100 by 5, we get:
55 ÷ 5 = 11 100 ÷ 5 = 20
Therefore, the simplified fraction is 11/20.
This means that 55% is equivalent to 11 parts out of 20 equal parts.
Practical Applications of 55% and 11/20
The ability to convert between percentages and fractions is crucial in various real-world scenarios. Here are a few examples where understanding this conversion is beneficial:
-
Calculating Discounts: If a store offers a 55% discount on an item, you can easily calculate the discount amount by multiplying the item's price by 11/20. This provides a quicker calculation than using the decimal equivalent (0.55).
-
Determining Proportions: If a survey shows that 55% of respondents prefer a particular product, you can represent this proportion as 11/20. This fractional representation can be more intuitive when comparing proportions or visualizing data.
-
Solving Mathematical Problems: Many mathematical problems involving percentages are often easier to solve using fractions. Converting the percentage to a fraction before carrying out calculations can simplify the process and reduce errors.
-
Understanding Financial Statements: Financial statements often present data as percentages. Converting these percentages to fractions can provide a clearer understanding of the ratios and proportions involved.
Further Exploration: Related Concepts and Conversions
Understanding the conversion of 55% to 11/20 lays the foundation for understanding other related concepts:
-
Decimal Equivalents: The fraction 11/20 can also be converted to a decimal by dividing the numerator by the denominator: 11 ÷ 20 = 0.55. This shows the direct relationship between percentages, fractions, and decimals.
-
Converting Other Percentages: The same method used for 55% can be applied to convert any percentage to a fraction. Simply write the percentage as a fraction over 100 and simplify.
-
Converting Fractions to Percentages: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, to convert 3/4 to a percentage, you would calculate (3 ÷ 4) x 100 = 75%.
-
Working with Improper Fractions: If you encounter a percentage greater than 100%, the resulting fraction will be an improper fraction (where the numerator is larger than the denominator). For instance, 150% is equivalent to 150/100, which simplifies to 3/2.
Illustrative Examples: Applying the Knowledge
Let's solidify our understanding with a couple of examples:
Example 1: A school has 200 students. 55% of them participate in extracurricular activities. How many students participate in extracurricular activities?
Solution: We can calculate this using the fraction 11/20. Multiply the total number of students by the fraction: 200 x (11/20) = 110 students.
Example 2: A retailer purchases goods for $500 and sells them at a 55% markup. What is the selling price?
Solution: The markup amount is $500 x (11/20) = $275. Therefore, the selling price is $500 + $275 = $775.
Frequently Asked Questions (FAQs)
Here are some frequently asked questions regarding the conversion of 55% to a fraction:
Q1: Why is simplifying the fraction important?
A1: Simplifying a fraction makes it easier to understand and work with. It presents the fraction in its most concise and efficient form. While 55/100 is correct, 11/20 is simpler and easier to use in calculations.
Q2: Can I use a calculator to simplify fractions?
A2: Yes, many calculators have a function to simplify fractions. Alternatively, you can use online fraction calculators or websites to simplify fractions quickly.
Q3: What if the percentage is a decimal, such as 55.5%?
A3: You would follow the same process. Write it as 55.5/100, and then you can either simplify by multiplying both the numerator and denominator by 10 to make it 555/1000 and then finding the GCD or converting it into a decimal and then to a fraction. The resulting fraction is 111/200.
Q4: Are there other ways to represent 55%?
A4: Yes, besides the fraction 11/20, you can represent 55% as a decimal (0.55) or a ratio (11:20).
Conclusion: Mastering the Conversion of Percentages to Fractions
Converting 55% to the fraction 11/20 is a fundamental skill with wide-ranging applications. Understanding this conversion enhances your mathematical capabilities and provides a more intuitive understanding of proportions, discounts, and various other numerical relationships. By mastering this seemingly simple conversion, you equip yourself with a powerful tool for tackling mathematical problems in various contexts, both academic and practical. Remember, the key is to write the percentage as a fraction over 100 and then simplify to its lowest terms. This approach forms the basis for converting any percentage to its fractional equivalent.
Latest Posts
Latest Posts
-
Is 164 A Perfect Square
Sep 16, 2025
-
How To Find Rhombus Diagonals
Sep 16, 2025
-
Whats 3 8 As A Decimal
Sep 16, 2025
-
Square Root Of 14 Simplified
Sep 16, 2025
-
How Do You Spell 150
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 55 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.