3x 2 X 3 X
keralas
Sep 15, 2025 · 6 min read
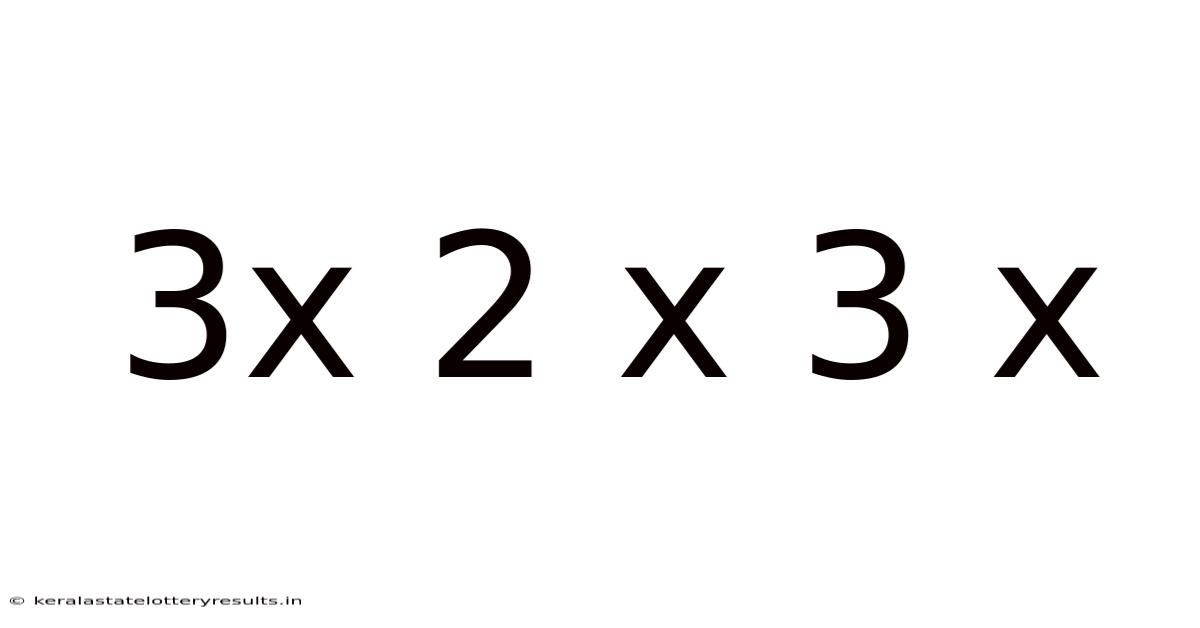
Table of Contents
Decoding the Mystery: A Deep Dive into 3 x 2 x 3 x ... and its Implications
This article explores the mathematical expression "3 x 2 x 3 x ..." and delves into its intriguing implications. At first glance, it appears deceptively simple, yet its true nature unfolds as we investigate different interpretations and approaches. We’ll examine the concept of infinite products, the role of convergence and divergence, and the fascinating connection to the realm of infinite series. Understanding this seemingly simple expression opens doors to a deeper appreciation of mathematical concepts like limits and infinity.
Understanding the Problem: The Ambiguity of an Incomplete Expression
The expression "3 x 2 x 3 x ..." is inherently incomplete. The ellipsis (...) indicates a continuation of the pattern, but without a defined endpoint or rule for the sequence, it's impossible to assign a single definitive value. This incompleteness is crucial. It highlights the importance of precise mathematical notation and the dangers of ambiguity. We must define the pattern's rule to proceed with any meaningful analysis. Several interpretations are possible, each leading to different results.
Interpretation 1: A Finite Product with an Implicit Ending
Let's assume the expression is a finite product, meaning the pattern continues for a specific, albeit unspecified, number of terms. For instance, we might consider:
- 3 x 2 x 3 x 2 x 3: This sequence alternates between 3 and 2. The result is 108.
- 3 x 2 x 3 x 2 x 3 x 2: Extending the sequence adds another 2, resulting in 216.
- 3 x 2 x 3 x 2 x 3 x 2 x 3: Adding another 3 brings the product to 648.
This interpretation allows for calculation, but the answer changes depending on the chosen length of the sequence. There's no inherent "correct" answer, only a result dependent on the arbitrary stopping point. This illustrates the critical need for explicit definitions in mathematics.
Interpretation 2: An Infinite Product – Introducing the Concept of Convergence
A more intriguing interpretation involves treating the expression as an infinite product. This necessitates the concept of convergence. An infinite product converges to a specific value if the partial products (products of the first n terms) approach a limit as n approaches infinity. If the partial products do not approach a limit, the infinite product diverges.
Let's consider a slightly modified, yet illustrative, infinite product: (3/2) x (3/2) x (3/2) x ... This can be represented as:
∏<sub>n=1</sub><sup>∞</sup> (3/2)
This product diverges because each term is greater than 1, causing the partial products to grow indefinitely without bound. They don't approach a specific limit.
However, consider a different infinite product: (1/2) x (2/3) x (3/4) x (4/5) x ... This product, represented as:
∏<sub>n=1</sub><sup>∞</sup> (n/(n+1))
This infinite product also diverges, but in this case, it approaches zero. The partial products get progressively smaller, getting closer and closer to zero, but never actually reaching it. This highlights the nuances of convergence: it's not simply about getting smaller; it's about approaching a specific finite limit.
Interpretation 3: Alternating Sequence – A More Complex Scenario
Let's revisit the original "3 x 2 x 3 x ..." and assume an alternating sequence of 3 and 2. This yields a product of the form:
3 x 2 x 3 x 2 x 3 x 2 x ...
This can be rewritten as:
(3 x 2) x (3 x 2) x (3 x 2) x ... = 6 x 6 x 6 x ... = ∏<sub>n=1</sub><sup>∞</sup> 6
This infinite product clearly diverges because it represents an infinite multiplication of 6. The partial products increase without bound.
The Importance of Convergence and Divergence
The concepts of convergence and divergence are fundamental in many areas of mathematics, including calculus, analysis, and probability. Understanding whether an infinite series or product converges or diverges is crucial for determining its value and its behavior. Various tests exist to determine convergence, including the ratio test, the root test, and the comparison test. These tests provide powerful tools for analyzing the behavior of infinite sequences.
For the initial expression "3 x 2 x 3 x...", without a defined pattern beyond the initial terms, we cannot definitively determine whether it converges or diverges, further emphasizing the necessity of precise mathematical definitions.
Connecting to Infinite Series: A Broader Perspective
Infinite products are closely related to infinite series. A series is a sum of infinitely many terms, while a product is a multiplication of infinitely many terms. Many techniques used to analyze infinite series can be adapted to analyze infinite products. Often, the logarithmic transformation is used to convert an infinite product into an infinite sum, which can then be analyzed using established techniques.
For example, consider the infinite product:
∏<sub>n=1</sub><sup>∞</sup> (1 + a<sub>n</sub>)
Taking the natural logarithm, we obtain the infinite sum:
∑<sub>n=1</sub><sup>∞</sup> ln(1 + a<sub>n</sub>)
If this sum converges, then the original product converges as well.
Practical Applications and Real-World Examples
While the expression "3 x 2 x 3 x ..." might seem abstract and purely theoretical, the concepts of infinite products and convergence have far-reaching applications:
- Calculus: Infinite products appear in various formulas and theorems within calculus, particularly in the study of infinite series and Taylor expansions.
- Probability and Statistics: Infinite products are essential in probability theory, for instance, in calculating probabilities related to infinite sequences of independent events.
- Physics: Infinite products and series often arise in physics when dealing with problems involving continuous processes or systems with infinitely many degrees of freedom. For example, certain calculations in quantum mechanics involve infinite products.
- Engineering: Analyzing convergence is crucial for many engineering applications, such as ensuring the stability of systems or modeling complex phenomena.
Frequently Asked Questions (FAQ)
-
Q: What is the exact value of "3 x 2 x 3 x ..."?
- A: There is no single exact value without defining the pattern's continuation and length. The expression is ambiguous without further clarification.
-
Q: How can I determine if an infinite product converges?
- A: Several convergence tests exist, such as the ratio test, the root test, and the comparison test. The choice of test depends on the specific form of the infinite product.
-
Q: What is the difference between an infinite series and an infinite product?
- A: An infinite series is an infinite sum, while an infinite product is an infinite multiplication. Both involve infinitely many terms, but their operations are different.
-
Q: Are infinite products always useful?
- A: No. If an infinite product diverges, it generally doesn't have a meaningful interpretation in the same way that a convergent product does.
Conclusion: The Beauty of Mathematical Precision
The seemingly simple expression "3 x 2 x 3 x ..." serves as a powerful illustration of the importance of precise mathematical notation and the critical role of convergence and divergence in the analysis of infinite products. While the initial ambiguity leaves the expression undefined, exploring its different interpretations sheds light on fundamental mathematical concepts with widespread applications across various fields. Understanding these concepts encourages a deeper appreciation of the elegance and power of mathematics. The lesson is clear: careful definition and rigorous analysis are crucial for navigating the fascinating world of infinite sequences and their implications. This seemingly simple problem opens a gateway to understanding sophisticated mathematical principles.
Latest Posts
Latest Posts
-
Whats 40 C In Fahrenheit
Sep 15, 2025
-
Is 2011 A Prime Number
Sep 15, 2025
-
One Fourth Plus One Fourth
Sep 15, 2025
-
What Times What Equals 100
Sep 15, 2025
-
5 9 In Metric System
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 X 3 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.