3 X 4.5 X 5
keralas
Sep 18, 2025 · 6 min read
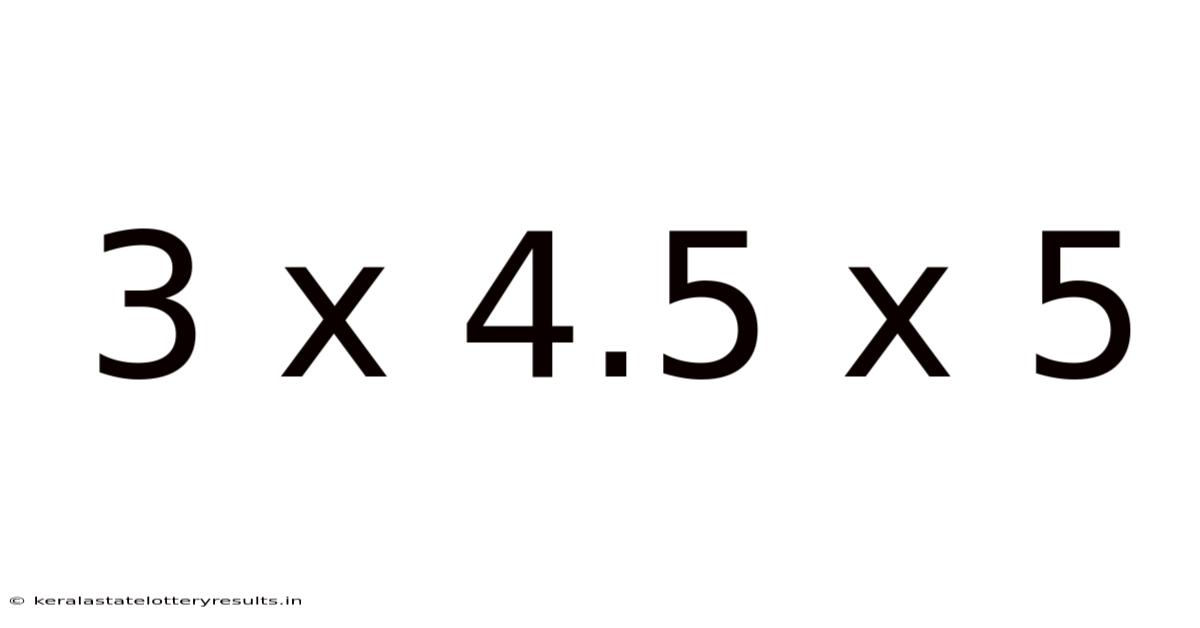
Table of Contents
Decoding the Dimensions: A Deep Dive into 3 x 4.5 x 5
The seemingly simple dimensions "3 x 4.5 x 5" might initially appear unremarkable. However, this seemingly mundane set of numbers opens a world of possibilities depending on the context. This article will explore the various interpretations and applications of these dimensions, delving into the mathematical concepts, practical applications, and even the potential for creative exploration. We'll uncover the significance of these dimensions across multiple fields, from the everyday to the specialized.
Understanding the Basics: Length, Width, and Height
Before we dive deeper, let's establish the fundamental understanding of what these numbers represent. In most contexts, "3 x 4.5 x 5" refers to three dimensions: length, width, and height. The order doesn't universally matter, but conventions often prioritize length first, followed by width, and finally height. Therefore, we can interpret these numbers as:
- Length: 3 units
- Width: 4.5 units
- Height: 5 units
The "units" here are crucial. Without specifying the unit of measurement (e.g., inches, centimeters, meters, feet), the dimensions remain abstract. This ambiguity highlights the importance of context when dealing with measurements.
Practical Applications Across Various Fields
The dimensions 3 x 4.5 x 5 can have a surprising number of real-world applications. Let’s explore some examples:
-
Packaging and Shipping: These dimensions are perfectly suitable for various packaging needs. Imagine a box designed to hold a specific product. The dimensions could dictate the size of the product itself, the internal space required for packaging materials (like bubble wrap or foam), and even the external dimensions for shipping labels and handling. The 3 x 4.5 x 5 dimensions might be ideal for a small appliance, a set of books, or a collection of smaller items. Optimizing the packaging dimensions directly impacts shipping costs and product protection.
-
Construction and Architecture: In construction, these dimensions could represent the size of a specific building element. It might be a small storage unit, a section of a wall, a window frame, or even a component within a larger structure. Precision in these measurements is vital for ensuring structural integrity and aesthetic appeal. The slightest discrepancy can have significant consequences.
-
Manufacturing and Engineering: In manufacturing, these dimensions could define the size of a component part for a larger machine or assembly. Think about the intricate parts of a clock, a piece of machinery, or even a simple toy. The accuracy of these dimensions is critical for the smooth functioning of the entire system. A slight deviation can lead to malfunction or failure.
-
3D Printing and Modeling: In the realm of 3D printing and 3D modeling, these dimensions define the size of a printable object. Designers frequently work with specific dimensions to create functional and aesthetically pleasing objects. The dimensions 3 x 4.5 x 5 could represent a small figurine, a model part, or a functional prototype. Accurate modeling is essential to ensure the final printed object meets expectations.
-
Gardening and Landscaping: These dimensions might describe the size of a planter box, a raised garden bed, or even a specific area within a larger garden layout. Understanding these dimensions is critical for proper planting, watering, and overall garden design. Careful consideration of space and proportions is vital for healthy plant growth.
Mathematical Explorations: Volume and Surface Area
Beyond their practical applications, the dimensions 3 x 4.5 x 5 offer opportunities for mathematical exploration. We can calculate the volume and surface area of a rectangular prism (or cuboid) with these dimensions:
Calculating Volume:
The volume of a rectangular prism is calculated using the formula:
Volume = Length × Width × Height
Substituting our dimensions, we get:
Volume = 3 × 4.5 × 5 = 67.5 cubic units.
Again, the "cubic units" emphasizes the three-dimensional nature of the volume. The unit (cubic inches, cubic centimeters, etc.) will depend on the units used for the original dimensions.
Calculating Surface Area:
The surface area of a rectangular prism is calculated as follows:
Surface Area = 2(Length × Width + Length × Height + Width × Height)
Substituting our dimensions:
Surface Area = 2(3 × 4.5 + 3 × 5 + 4.5 × 5) = 2(13.5 + 15 + 22.5) = 2(51) = 102 square units.
Understanding both volume and surface area is crucial in various applications. For instance, in packaging, the volume determines the amount of space available, while the surface area affects the amount of material needed for packaging. In construction, surface area is important for estimating the amount of paint or material needed to cover a surface.
Scaling and Proportionality:
The dimensions 3 x 4.5 x 5 can be scaled up or down proportionally. This means multiplying or dividing all three dimensions by the same factor. For instance, multiplying each dimension by 2 would result in dimensions of 6 x 9 x 10. This maintains the same proportions but increases the overall size. Conversely, dividing by 2 would result in smaller dimensions of 1.5 x 2.25 x 2.5. This principle of scaling is fundamental in various design and engineering applications.
Creative Explorations: Beyond the Practical
Beyond the practical applications, these dimensions can inspire creative explorations. Artists, designers, and architects might use these proportions to create aesthetically pleasing forms or functional designs. The ratio between the dimensions can influence the overall visual impact and the way the object interacts with its surroundings.
FAQs
Q: What are the units of measurement for these dimensions?
A: The units are not specified. The dimensions "3 x 4.5 x 5" are abstract without specifying the unit (e.g., inches, centimeters, meters).
Q: Can these dimensions be used for something other than a rectangular prism?
A: While these dimensions primarily describe a rectangular prism, they could indirectly relate to other shapes. For example, they might represent the bounding box of a more complex three-dimensional object.
Q: How do I calculate the diagonal of this rectangular prism?
A: The diagonal of a rectangular prism is calculated using the formula: √(Length² + Width² + Height²). In this case, the diagonal would be √(3² + 4.5² + 5²) ≈ 7.3 units.
Q: What are some real-world examples where these dimensions are actually used?
A: While precise examples require knowing the units, these dimensions are frequently used in various fields. Examples include small appliance packaging, components in manufacturing, building blocks, and 3D-printed models.
Conclusion: The Significance of the Seemingly Simple
The seemingly simple dimensions 3 x 4.5 x 5 represent a gateway to a deeper understanding of measurement, geometry, and their multifaceted applications. From the practical considerations of packaging and construction to the creative explorations of art and design, these dimensions highlight the interplay between mathematics and the real world. The precision and accuracy in handling these numbers are fundamental across various industries, demonstrating the significance of seemingly simple numerical values. The exploration of these dimensions allows for a richer understanding of concepts applicable in numerous fields, highlighting their importance in both practical and creative pursuits. This comprehensive exploration underlines the value of understanding even the most basic dimensional specifications and their implications in various disciplines.
Latest Posts
Latest Posts
-
What Is 3 Times 6
Sep 18, 2025
-
How Far Is 2000 Yards
Sep 18, 2025
-
Factor X 2 X 2
Sep 18, 2025
-
What Is 4 Times 9
Sep 18, 2025
-
How Much Is 8 Qt
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 X 4.5 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.