3 To 1 In Percentage
keralas
Sep 14, 2025 · 6 min read
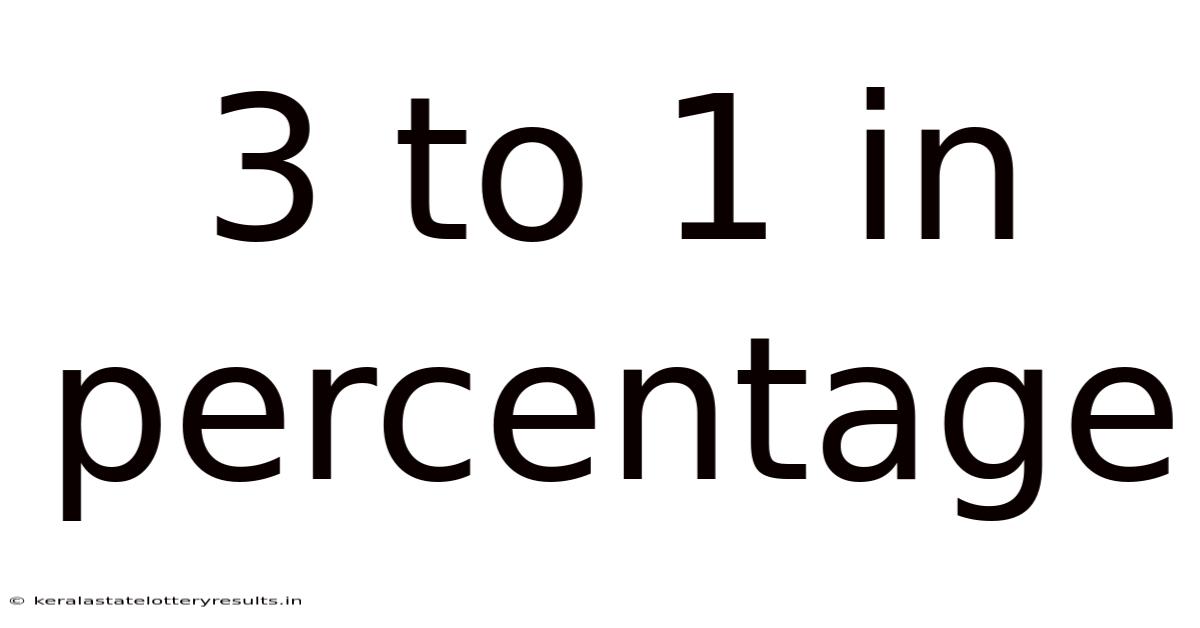
Table of Contents
Understanding the 3:1 Ratio and its Percentage Equivalent: A Comprehensive Guide
The ratio 3:1 is a fundamental concept in mathematics and finds applications across various fields, from finance and engineering to cooking and art. Understanding how to express this ratio as a percentage is crucial for accurate calculations and effective communication of proportional relationships. This article will provide a comprehensive explanation of the 3:1 ratio, its conversion to percentage, and diverse practical applications, ensuring a thorough understanding for readers of all backgrounds. We'll delve into the calculations, explore different scenarios where this ratio appears, and address common questions.
Understanding Ratios
Before diving into the specifics of the 3:1 ratio, let's establish a solid understanding of ratios themselves. A ratio is a mathematical comparison between two or more quantities. It shows the relative sizes of the quantities. For example, a ratio of 2:1 means there are two parts of one quantity for every one part of another. Ratios can be expressed in different ways: using a colon (e.g., 3:1), as a fraction (e.g., 3/1), or as a decimal (e.g., 3.0).
Deconstructing the 3:1 Ratio
The ratio 3:1 signifies that for every one unit of the second quantity, there are three units of the first quantity. This implies a significant difference in magnitude between the two quantities involved. The ratio remains consistent regardless of the units used; whether it's 3 apples to 1 orange, 3 kilograms to 1 kilogram, or 3 dollars to 1 dollar, the proportional relationship stays the same.
Converting 3:1 to Percentage
Converting a ratio to a percentage involves understanding that a percentage represents a fraction out of 100. To convert the 3:1 ratio to a percentage, we follow these steps:
-
Express the ratio as a fraction: The ratio 3:1 can be written as the fraction 3/1.
-
Find the equivalent fraction with a denominator of 100: To express this as a percentage (out of 100), we need to find an equivalent fraction where the denominator is 100. We can achieve this by multiplying both the numerator and the denominator by a common factor. In this case, we would divide the numerator by the denominator, then multiply by 100%. Thus: (3/1) * 100% = 300%.
Therefore, the 3:1 ratio is equivalent to 300%. This means the first quantity is 300% of the second quantity, or three times the size of the second quantity.
Practical Applications of the 3:1 Ratio and its Percentage Equivalent
The 3:1 ratio, and its 300% representation, appears in various contexts:
-
Finance and Investments: Imagine an investment that yields a 3:1 return. For every dollar invested, you receive three dollars in profit. This represents a 300% return on investment (ROI).
-
Engineering and Construction: In structural design, specific material ratios might be crucial for strength and stability. A 3:1 concrete mix, for example, might indicate a specific proportion of cement to aggregate.
-
Mixing and Recipes: In cooking and baking, ratios are essential for consistent results. A 3:1 ratio of flour to water in a particular recipe ensures the desired consistency.
-
Medical Dosage: While less common as a direct ratio, the underlying principle of proportions is vital in determining dosages of medications based on weight or other physiological factors.
-
Sports and Statistics: In various sports, ratios can be used to analyze player performance or team strategies. A 3:1 ratio in goal scoring might illustrate a team's superior offensive capabilities.
-
Art and Design: In art and design, proportions play a critical role in composition and aesthetics. The 3:1 ratio might be utilized to create visual balance or emphasize specific elements within a design.
-
Environmental Science: Pollution levels can sometimes be represented using ratios, comparing the concentration of a pollutant to a baseline level. A 3:1 ratio might indicate a significantly elevated pollution level.
Beyond Simple Ratios: Considering More Complex Scenarios
While the 3:1 ratio is straightforward, understanding its application in more complex scenarios requires careful consideration. For instance, imagine a situation with a larger ratio like 300:100. While seemingly different, this ratio simplifies to 3:1 and maintains the same 300% relationship. The importance lies in simplifying the ratio to its fundamental form for easy interpretation.
Consider another scenario: You have a mixture containing 3 parts substance A and 1 part substance B. The total mixture comprises 4 parts (3 + 1). If you want to find the percentage of substance A in the mixture, you would calculate (3/4) * 100% = 75%. This highlights the importance of differentiating between the ratio of the two individual substances and the percentage composition within the entire mixture.
Frequently Asked Questions (FAQ)
Q1: How do I convert a percentage back to a ratio?
A1: To convert a percentage to a ratio, simply divide the percentage by 100 and simplify the resulting fraction. For instance, 75% becomes 75/100, which simplifies to 3/4, or a 3:4 ratio. For 300%, this would be 300/100 = 3/1 or a 3:1 ratio.
Q2: Can a ratio have a percentage greater than 100%?
A2: Yes, absolutely. A percentage greater than 100% simply indicates that one quantity is larger than another. The 3:1 ratio, equivalent to 300%, exemplifies this perfectly.
Q3: What if I have a ratio with more than two quantities?
A3: Ratios can involve more than two quantities. For example, a 2:3:1 ratio implies two parts of one quantity, three parts of a second, and one part of a third. The calculations for converting these to percentages become slightly more involved but follow the same principles of finding equivalent fractions with a common denominator.
Q4: Are there any limitations to using percentages to represent ratios?
A4: While percentages are widely used, they can sometimes be less intuitive than ratios, especially when dealing with very large or very small numbers. Ratios offer a clear representation of the relative proportions, which can be beneficial in certain contexts. Additionally, the use of percentages sometimes necessitates the use of decimals for increased accuracy, adding a layer of complexity that may not be present when using simple ratios.
Q5: How can I ensure I'm using the correct percentage when dealing with ratios?
A5: Always clearly identify which quantity is being expressed as a percentage in relation to which other quantity. Carefully consider the context of the problem and ensure your calculations accurately reflect the relationship between the quantities involved. Double-checking your work and using visual aids, such as diagrams or charts, can help reduce errors.
Conclusion
The 3:1 ratio, equivalent to 300%, is a fundamental concept with broad applications. Understanding its conversion to percentage and its implications in various contexts is essential for anyone working with proportions, whether in finance, engineering, cooking, or other fields. This article has provided a comprehensive exploration of the topic, equipping readers with the knowledge and skills to confidently interpret and utilize this important mathematical relationship. Remember to always clearly define the quantities involved and carefully execute the calculations to avoid misinterpretations and ensure accurate results in any application. By understanding the underlying principles and practicing these concepts, you can build a stronger foundation in mathematical reasoning and proportional analysis.
Latest Posts
Latest Posts
-
Convert 0 75 To A Fraction
Sep 14, 2025
-
Simplest Radical Form Of 48
Sep 14, 2025
-
Lcd Of 7 And 9
Sep 14, 2025
-
Sin 60 As A Fraction
Sep 14, 2025
-
What Shape Has 20 Sides
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 To 1 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.