25/3 As A Mixed Number
keralas
Sep 13, 2025 · 5 min read
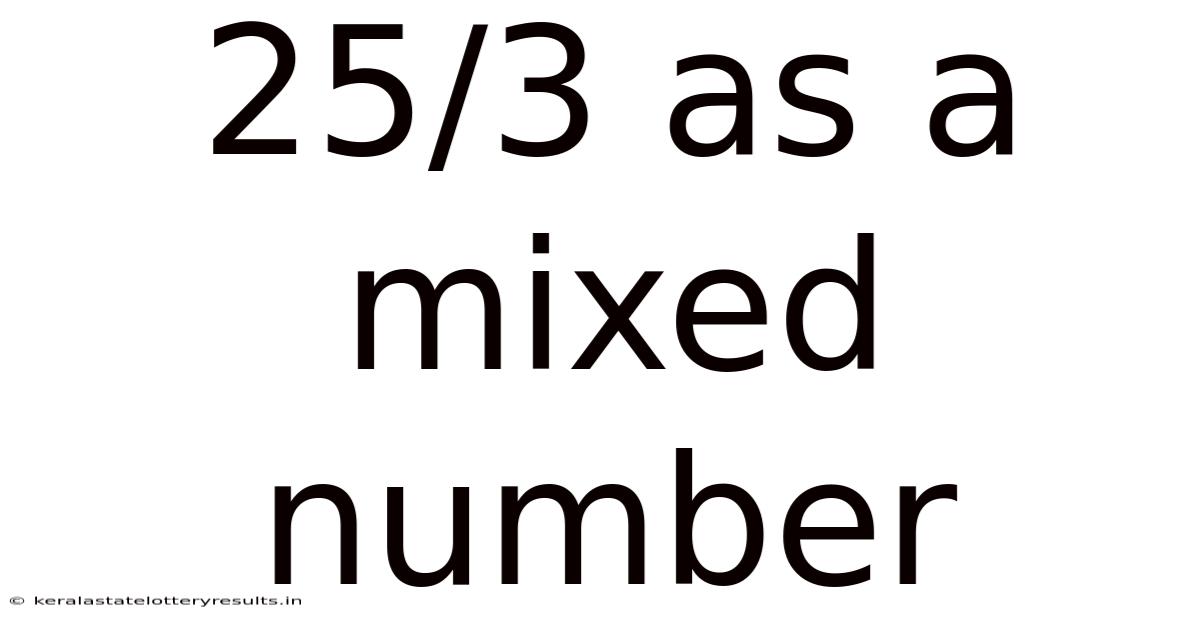
Table of Contents
Understanding 25/3 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 25/3 might appear straightforward at first glance. However, understanding its representation as a mixed number unlocks a deeper understanding of fractional arithmetic and its practical applications. This comprehensive guide will not only show you how to convert 25/3 into a mixed number but will also explore the underlying concepts, provide practical examples, and answer frequently asked questions. This guide is designed for students of all levels, from those just beginning to grasp fractions to those seeking a more robust understanding of mathematical concepts.
Introduction to Fractions and Mixed Numbers
Before diving into the conversion of 25/3, let's refresh our understanding of fractions and mixed numbers. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows the total number of equal parts the whole is divided into.
A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). It represents a quantity that is greater than one. For example, 2 ½ is a mixed number, indicating two whole units and an additional half.
Converting 25/3 to a Mixed Number: Step-by-Step
The process of converting an improper fraction (like 25/3, where the numerator is larger than the denominator) into a mixed number involves division. Here's the step-by-step process:
-
Divide the numerator by the denominator: Divide 25 by 3. This gives us a quotient (the whole number part of the mixed number) and a remainder.
25 ÷ 3 = 8 with a remainder of 1
-
Identify the whole number: The quotient (8) becomes the whole number part of our mixed number.
-
Identify the fractional part: The remainder (1) becomes the numerator of the fractional part. The denominator remains the same as the original fraction (3).
-
Combine the whole number and the fraction: The result is the mixed number 8 ⅓.
Therefore, 25/3 expressed as a mixed number is 8 ⅓.
Visual Representation and Real-World Application
Understanding fractions and mixed numbers can be significantly enhanced through visualization. Imagine you have 25 identical cookies. If you want to divide these cookies equally among 3 friends, how many cookies would each friend get?
By dividing 25 by 3, we find that each friend gets 8 whole cookies (8 x 3 = 24 cookies). There's 1 cookie left over (25 - 24 = 1 cookie), which needs to be divided equally among the 3 friends. This leftover cookie represents the fractional part, ⅓. Thus, each friend receives 8 ⅓ cookies. This real-world example vividly demonstrates the practical application of converting an improper fraction to a mixed number.
Further Exploration: Equivalent Fractions
It's crucial to understand that 25/3 and 8 ⅓ represent the same quantity. They are equivalent fractions. We can convert a mixed number back to an improper fraction using the following steps:
-
Multiply the whole number by the denominator: 8 x 3 = 24
-
Add the numerator: 24 + 1 = 25
-
Keep the same denominator: The denominator remains 3.
This results in the improper fraction 25/3, confirming the equivalence.
The Importance of Understanding Mixed Numbers
Mixed numbers are essential in various mathematical contexts and everyday situations:
-
Measurement: When measuring lengths, weights, or volumes, we often encounter mixed numbers. For instance, a board might measure 8 ⅓ feet long.
-
Cooking and Baking: Recipes frequently use mixed numbers to specify ingredient quantities (e.g., 2 ½ cups of flour).
-
Time: Time is often expressed using mixed numbers (e.g., 2 ¾ hours).
-
Advanced Mathematics: A strong understanding of mixed numbers is foundational for more complex mathematical operations like addition, subtraction, multiplication, and division of fractions.
Different Methods of Converting Improper Fractions to Mixed Numbers
While the division method explained above is the most common and straightforward, there are other approaches to converting improper fractions to mixed numbers:
-
Repeated Subtraction: You can repeatedly subtract the denominator from the numerator until the remainder is less than the denominator. The number of times you subtract represents the whole number, and the remainder forms the numerator of the fraction.
-
Using a Number Line: You can visualize the conversion on a number line. Mark the whole numbers and then divide the intervals between them into equal parts based on the denominator. Locate the fraction on the number line to see its equivalent mixed number representation.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert improper fractions to mixed numbers?
A1: Converting improper fractions to mixed numbers helps us better understand and visualize quantities greater than one. It also simplifies calculations and makes it easier to apply fractions in real-world situations.
Q2: Can all improper fractions be converted into mixed numbers?
A2: Yes, all improper fractions can be converted into mixed numbers. The process always involves dividing the numerator by the denominator.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, the improper fraction is a whole number. There is no fractional part in the mixed number. For example, 12/3 = 4.
Q4: Are there any situations where it's better to leave a fraction as an improper fraction?
A4: In certain mathematical operations, particularly multiplication and division of fractions, it can be simpler to work with improper fractions rather than mixed numbers.
Q5: How can I practice converting improper fractions to mixed numbers?
A5: Practice with various examples. Start with simple improper fractions and gradually increase the complexity. Use online resources, workbooks, or educational apps for extra practice.
Conclusion: Mastering Fractions for a Brighter Future
Converting 25/3 to the mixed number 8 ⅓ is more than just a simple mathematical operation. It represents a crucial step in understanding the fundamental concepts of fractions and their practical applications in numerous fields. By mastering this conversion, you enhance your numerical literacy and build a solid foundation for more advanced mathematical concepts. Remember that practice is key. The more you work with fractions and mixed numbers, the more comfortable and confident you will become in using them effectively. Embrace the challenge, and watch your mathematical skills flourish!
Latest Posts
Latest Posts
-
What Is 0 05 In Percentage
Sep 13, 2025
-
Gcf Of 64 And 72
Sep 13, 2025
-
Gcf Of 96 And 84
Sep 13, 2025
-
Gcf Of 15 And 24
Sep 13, 2025
-
What Times What Equals 112
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 25/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.