2 Times What Equals 30
keralas
Sep 14, 2025 · 5 min read
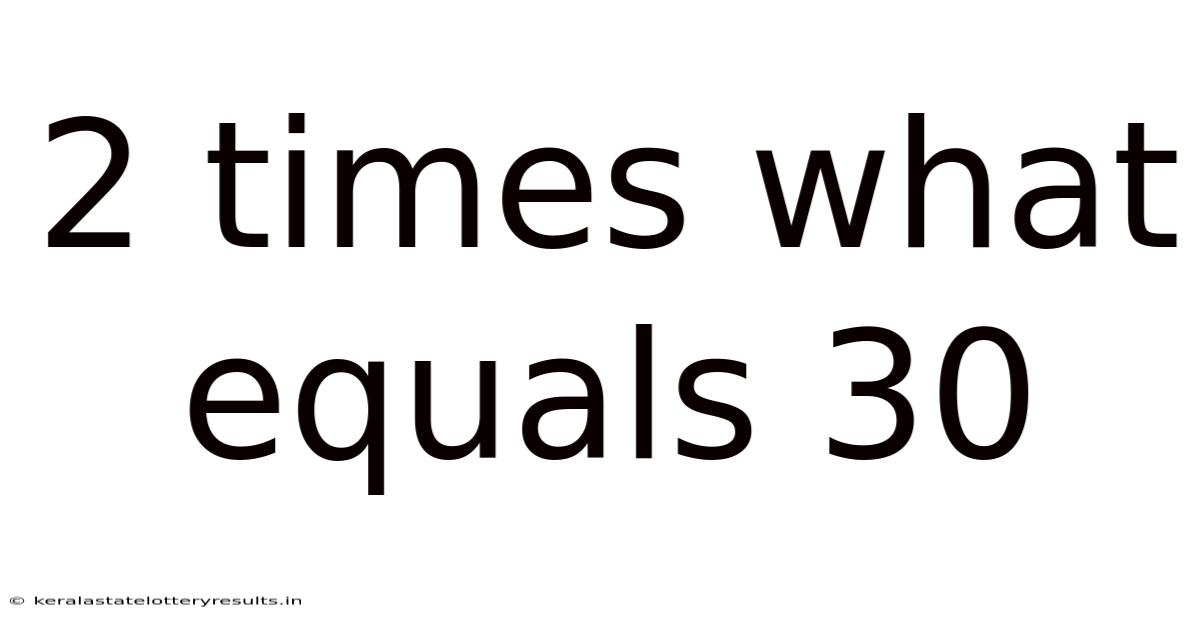
Table of Contents
Decoding "2 Times What Equals 30": A Deep Dive into Multiplication and Problem-Solving
Finding the answer to "2 times what equals 30" might seem simple at first glance, but it opens the door to exploring fundamental mathematical concepts, problem-solving strategies, and even the fascinating world of algebra. This article will not only provide the solution but also delve into the underlying principles, explore different approaches to solving similar problems, and address frequently asked questions. Understanding this seemingly basic equation is crucial for building a strong foundation in mathematics.
Understanding the Problem: Multiplication and the Unknown
The question, "2 times what equals 30," presents a simple multiplication problem with one unknown element. In mathematical terms, we can represent it as an equation: 2 * x = 30. Here, 'x' represents the unknown number we need to find. The asterisk (*) symbolizes multiplication, and the equals sign (=) indicates that both sides of the equation are equal in value. Understanding this basic structure is key to solving the problem and similar equations.
Solving the Equation: Direct Approach
The most straightforward method to solve 2 * x = 30 involves isolating the unknown variable 'x'. We achieve this by performing the inverse operation of multiplication, which is division. Since 2 is multiplied by x, we divide both sides of the equation by 2:
(2 * x) / 2 = 30 / 2
This simplifies to:
x = 15
Therefore, the answer to "2 times what equals 30" is 15.
Alternative Approaches: Visualizing and Reasoning
While the algebraic method is efficient, we can also approach this problem using visualization and logical reasoning. Imagine you have two identical groups of items, and the total number of items in both groups is 30. To find the number of items in each group, you would divide the total (30) by the number of groups (2). This leads us to the same answer: 15 items per group. This approach is particularly helpful for beginners who are still developing their algebraic skills.
Expanding the Concept: Introduction to Algebra
The equation 2 * x = 30 is a simple algebraic equation. Algebra involves using letters (variables) to represent unknown quantities. Solving algebraic equations involves manipulating the equation to isolate the variable and determine its value. This seemingly simple equation lays the groundwork for more complex algebraic problems encountered in higher-level mathematics. Mastering this fundamental concept is essential for success in algebra and other related fields.
Solving Similar Problems: Varying the Numbers
Understanding the principle behind solving "2 times what equals 30" allows us to solve similar problems with different numbers. For example:
-
3 times what equals 27? Following the same process, we divide 27 by 3, resulting in x = 9.
-
5 times what equals 45? Dividing 45 by 5 gives us x = 9.
-
10 times what equals 100? Dividing 100 by 10 yields x = 10.
By consistently applying the principle of division to isolate the unknown variable, we can solve a wide range of multiplication problems.
Real-World Applications: Practical Examples
The concept of "2 times what equals 30" isn't just confined to mathematical exercises. It has numerous real-world applications:
-
Sharing equally: If you have 30 candies and want to share them equally between 2 friends, each friend gets 15 candies.
-
Pricing: If two identical items cost $30 in total, each item costs $15.
-
Measurement: If two lengths combined measure 30 centimeters, each length is 15 centimeters.
These examples highlight how understanding basic multiplication and algebraic equations can help us solve everyday problems efficiently.
Beyond the Basics: Exploring More Complex Equations
While "2 times what equals 30" represents a simple equation, it forms the foundation for tackling more complex mathematical problems. Consider these extensions:
-
Equations with multiple operations: Problems like "2 times a number plus 5 equals 35" require a multi-step approach, involving subtraction and division.
-
Equations with unknowns on both sides: Equations like "2x + 5 = x + 10" require more manipulation to isolate the variable.
-
Simultaneous equations: Solving systems of equations with multiple variables and equations requires a deeper understanding of algebraic manipulation.
Mastering the fundamentals allows for a smoother transition to these more complex scenarios.
Frequently Asked Questions (FAQ)
Q: What is the inverse operation of multiplication?
A: The inverse operation of multiplication is division. They essentially "undo" each other.
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to divide 30 by 2 to get the answer quickly. However, understanding the underlying mathematical principle is crucial for solving more complex problems.
Q: What if the equation was 2x - 5 = 25?
A: In this case, you would first add 5 to both sides to get 2x = 30, then divide by 2 to find x = 15. This illustrates the need for step-by-step manipulation in solving equations.
Q: Why is understanding this type of problem important?
A: Understanding simple algebraic equations like this forms a foundation for more advanced mathematical concepts. It helps develop problem-solving skills applicable across many areas of life, not just mathematics.
Q: Are there any other methods to solve this problem?
A: Yes, you could use trial and error, repeatedly multiplying 2 by different numbers until you reach 30. However, the algebraic method is more efficient and systematic.
Conclusion: Building a Solid Mathematical Foundation
The seemingly simple question, "2 times what equals 30," provides a gateway to exploring essential mathematical concepts. From understanding basic multiplication and the inverse operation of division to grasping the fundamentals of algebra, this problem highlights the importance of building a strong mathematical foundation. The ability to solve such equations effectively is crucial not only for academic success but also for navigating various real-world scenarios that require logical reasoning and problem-solving skills. By mastering these fundamental concepts, you empower yourself to tackle increasingly complex mathematical challenges with confidence and proficiency. Remember, the key is not just to find the answer (which is 15) but to understand how you arrived at that answer and the broader mathematical principles it embodies.
Latest Posts
Latest Posts
-
Find Derivative Of An Integral
Sep 14, 2025
-
What Are The Factors 72
Sep 14, 2025
-
Different Types Of Scatter Graphs
Sep 14, 2025
-
Is 397 A Prime Number
Sep 14, 2025
-
What Is 0 05 In Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 Times What Equals 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.