2 Percent As A Fraction
keralas
Sep 17, 2025 · 5 min read
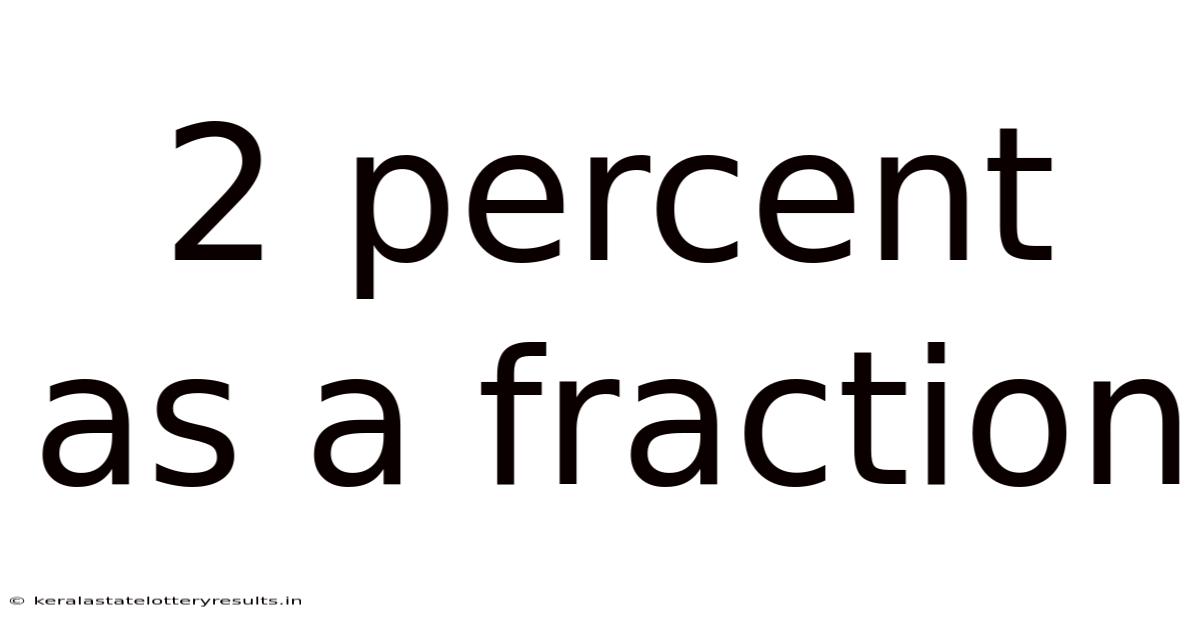
Table of Contents
Understanding 2 Percent as a Fraction: A Comprehensive Guide
2% might seem like a simple concept, but understanding it deeply opens doors to a broader comprehension of percentages, fractions, decimals, and their interconnectedness. This article will explore 2 percent as a fraction in detail, delving into its various representations, applications, and the underlying mathematical principles. We'll cover everything from basic conversions to more advanced concepts, ensuring a thorough understanding for learners of all levels.
Introduction: Percentages, Fractions, and Decimals – A Unified Family
Before diving into the specifics of 2%, let's establish the fundamental relationships between percentages, fractions, and decimals. They are essentially different ways of expressing the same proportional value. A percentage represents a fraction of 100, a fraction expresses a part of a whole, and a decimal uses base-ten notation to represent a numerical value. Understanding this interconnectedness is key to mastering these concepts.
For instance, 2% means 2 out of every 100 parts. This can be written as a fraction (2/100) or a decimal (0.02). The ability to convert between these three forms is crucial for solving various mathematical problems and understanding real-world applications.
Converting 2 Percent to a Fraction: A Step-by-Step Guide
Converting 2% to a fraction is a straightforward process. Remember, the percent sign (%) signifies "per hundred." Therefore, 2% directly translates to the fraction 2/100.
Step 1: Write the Percentage as a Fraction
As mentioned above, 2% can be written as the fraction 2/100. This is the most basic representation.
Step 2: Simplify the Fraction (if possible)
This step involves finding the greatest common divisor (GCD) of the numerator (2) and the denominator (100) and dividing both by it. The GCD of 2 and 100 is 2. Dividing both the numerator and the denominator by 2, we get:
2/100 = 1/50
Therefore, the simplest form of the fraction representing 2% is 1/50.
Different Representations of 2%
While 1/50 is the simplest form, it's important to understand that 2% can be represented by other equivalent fractions. These fractions all represent the same proportional value, but their numerators and denominators are different. For example:
- 2/100: This is the direct conversion from the percentage.
- 4/200: Multiplying both the numerator and the denominator of 1/50 by 4.
- 6/300: Multiplying both the numerator and the denominator of 1/50 by 6.
- 10/500: Multiplying both the numerator and the denominator of 1/50 by 10.
And so on. While all these fractions are equivalent to 2%, 1/50 is preferred due to its simplicity. This illustrates the importance of simplifying fractions to their lowest terms for clarity and ease of calculation.
Understanding the Concept of Proportionality
The core of understanding percentages and fractions lies in grasping the concept of proportionality. A percentage represents a part of a whole, expressed as a ratio out of 100. The fraction 1/50 represents the same proportion, but in a different form. It indicates that one part out of 50 equal parts represents the same proportion as 2 out of 100 equal parts.
Imagine a pie cut into 100 slices. 2% represents 2 of those slices. Now imagine a smaller pie cut into 50 slices. 1/50 represents one of those slices. Both scenarios represent the same proportional amount of pie. This illustrates the equivalence between 2% and 1/50.
Real-World Applications of 2%
Understanding 2% as a fraction has numerous real-world applications:
-
Financial Calculations: Interest rates, discounts, tax calculations, and profit margins often involve percentages. Converting percentages to fractions simplifies these calculations. For example, calculating 2% interest on a loan requires converting 2% to 1/50 for easier computation.
-
Scientific Measurements: In scientific contexts, percentages are frequently used to represent proportions or changes. Converting them to fractions provides a more precise and manageable form for analysis and calculations.
-
Data Analysis: Representing data as percentages and subsequently fractions helps in visualizing and interpreting proportions within datasets. This is crucial in fields like statistics and demographics.
-
Everyday Life: Discounts in stores, ingredient proportions in recipes, and even estimating tips all involve working with percentages which are often easier to understand and calculate when converted to fractions.
Further Exploration: Converting to Decimals
While we focused on fractions, it's equally important to understand the decimal equivalent of 2%. As mentioned earlier, 2% is equivalent to 0.02. This decimal representation is obtained by dividing the percentage by 100. This is another essential representation for various calculations, especially those involving digital tools and calculators.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand, compare, and use in calculations. It presents the proportion in its most concise and efficient form.
Q2: Can I convert any percentage to a fraction?
A2: Yes, absolutely. Any percentage can be converted into a fraction by writing the percentage value over 100 and then simplifying.
Q3: What if the percentage is a decimal, like 2.5%?
A3: You can still convert it to a fraction. 2.5% can be written as 2.5/100. Multiplying both numerator and denominator by 10 to remove the decimal gives 25/1000. Simplifying this fraction yields 1/40.
Q4: Are there any limitations to representing a percentage as a fraction?
A4: While fractions offer a precise representation of proportions, very large or complex percentages might lead to unwieldy fractions. In such cases, decimals might be a more practical alternative. However, this doesn't diminish the utility of fractions in general.
Q5: How can I improve my understanding of percentages and fractions?
A5: Practice is key! Try converting various percentages to fractions and decimals. Work through problems involving these concepts in different contexts. Utilizing online resources, educational videos, and interactive exercises can also greatly enhance your understanding.
Conclusion: Mastering the Interplay of Percentages, Fractions, and Decimals
Understanding 2% as a fraction is not just about memorizing a simple conversion (2% = 1/50). It's about understanding the fundamental relationships between percentages, fractions, and decimals. By grasping the concept of proportionality and practicing conversions, you build a strong foundation for tackling more complex mathematical problems and real-world applications involving ratios and proportions. This knowledge is not only valuable in academic settings but also essential for navigating various aspects of daily life and professional endeavors. The ability to seamlessly translate between these three forms of representation makes you more adaptable and proficient in tackling numerical challenges. Remember that continuous practice and exploration will solidify your understanding and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
Lcm Of 24 And 8
Sep 17, 2025
-
Gcf Of 15 And 36
Sep 17, 2025
-
What Is Multiple Of 12
Sep 17, 2025
-
Reference Angle For Negative Angles
Sep 17, 2025
-
Area Of The Shaded Sector
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.