2 3 5 7 11
keralas
Sep 14, 2025 · 6 min read
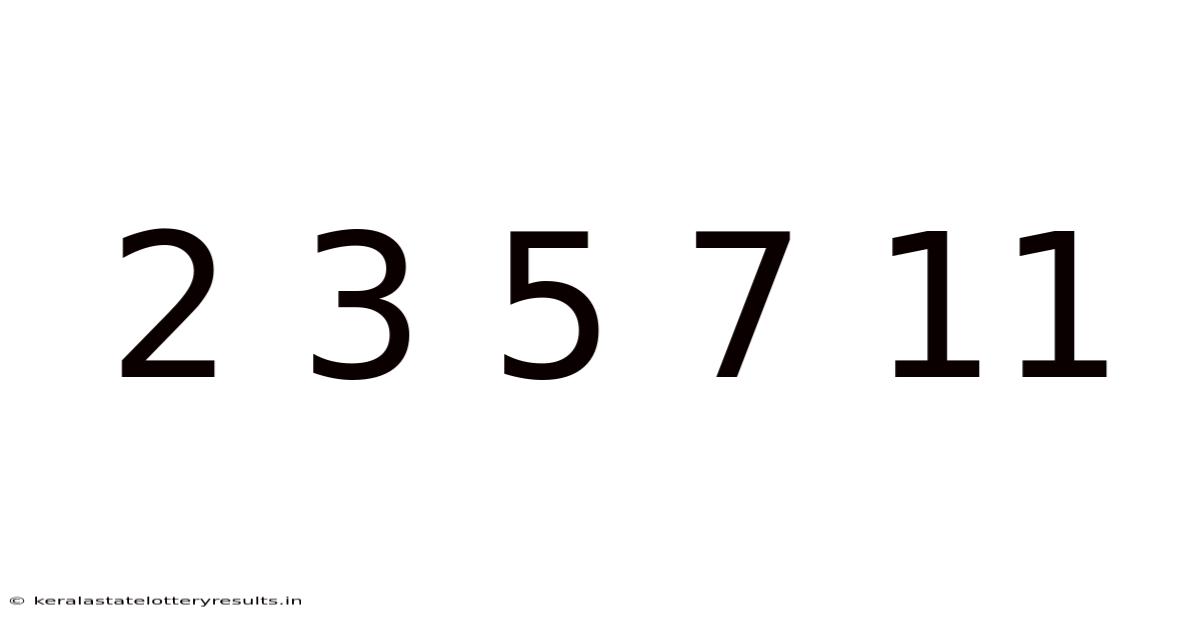
Table of Contents
Unveiling the Secrets of 2, 3, 5, 7, and 11: A Deep Dive into Prime Numbers and Beyond
The seemingly simple sequence 2, 3, 5, 7, and 11 might appear unremarkable at first glance. However, these numbers hold a profound significance in mathematics, representing the first five prime numbers. This article will delve into the fascinating world of prime numbers, exploring their properties, their importance in various mathematical fields, and their surprising applications in areas far beyond the realm of pure mathematics. We’ll uncover what makes them special, how they're identified, and why understanding them is crucial for various aspects of our world, from cryptography to computer science.
Understanding Prime Numbers: The Building Blocks of Arithmetic
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, a prime number is only divisible by 1 and itself. Our initial sequence, 2, 3, 5, 7, and 11, perfectly exemplifies this definition. 2 is divisible only by 1 and 2; 3 only by 1 and 3; and so on. Numbers that are not prime are called composite numbers. For instance, 4 (2 x 2), 6 (2 x 3), 8 (2 x 4), and 9 (3 x 3) are composite numbers because they can be factored into smaller natural numbers.
The fundamental theorem of arithmetic states that every integer greater than 1 is either a prime number itself or can be uniquely represented as a product of prime numbers. This means prime numbers are the fundamental building blocks of all other numbers, much like atoms are the building blocks of matter. This principle is foundational to numerous mathematical concepts and operations.
Identifying Prime Numbers: Methods and Algorithms
Determining whether a large number is prime can be surprisingly challenging. While simple inspection works for smaller numbers, more sophisticated methods are required for larger ones. Several algorithms exist for primality testing, with varying levels of efficiency:
-
Trial Division: This is the most straightforward method. It involves dividing the number by all prime numbers up to its square root. If none of these divisions result in a whole number, the number is prime. This method is simple but inefficient for very large numbers.
-
Sieve of Eratosthenes: This is an ancient algorithm that efficiently generates all prime numbers up to a specified limit. It works by iteratively marking the multiples of each prime number, leaving only the prime numbers unmarked. It's highly efficient for finding primes within a given range.
-
Probabilistic Tests: For extremely large numbers, probabilistic tests are employed. These tests don't guarantee primality with absolute certainty but provide a very high probability. The Miller-Rabin test is a popular example. These tests are crucial in cryptography, where dealing with astronomically large prime numbers is commonplace.
The Distribution of Prime Numbers: The Prime Number Theorem
Prime numbers are not evenly distributed along the number line. Their frequency decreases as numbers get larger. However, their distribution is not entirely random. The Prime Number Theorem provides a remarkable approximation of the number of primes less than or equal to a given number. It states that the number of primes less than or equal to x is approximately x / ln(x), where ln(x) is the natural logarithm of x. This theorem, though seemingly simple, is a profound result that reveals a deep underlying order in the seemingly chaotic distribution of prime numbers. It’s a testament to the elegance and interconnectedness within the realm of number theory.
The Significance of Prime Numbers in Cryptography
The unique properties of prime numbers form the cornerstone of modern cryptography. RSA encryption, one of the most widely used public-key cryptosystems, relies heavily on the difficulty of factoring large numbers into their prime components. The security of RSA depends on the fact that multiplying two large prime numbers is computationally easy, while factoring the resulting product back into its prime factors is incredibly difficult, even for the most powerful computers. This asymmetry forms the basis of secure communication and data protection across the internet. The larger the prime numbers used, the more secure the encryption becomes.
Beyond Cryptography: Applications in Other Fields
The influence of prime numbers extends far beyond cryptography. Their applications permeate various fields:
-
Computer Science: Prime numbers play a crucial role in hash tables, a fundamental data structure used for efficient data retrieval. Prime numbers are often used as the size of hash tables to minimize collisions and maximize efficiency.
-
Coding Theory: Prime numbers are used in error-correcting codes, which are essential for reliable data transmission and storage. These codes help detect and correct errors that might occur during transmission, ensuring data integrity.
-
Number Theory Research: Prime numbers are a central focus of ongoing research in number theory. Unanswered questions about their distribution, such as the twin prime conjecture (which postulates that there are infinitely many pairs of prime numbers that differ by 2, like 3 and 5, or 11 and 13), continue to drive mathematical exploration. The Riemann Hypothesis, one of the most important unsolved problems in mathematics, is directly related to the distribution of prime numbers.
-
Physics: While less directly involved, the principles governing prime numbers have inspired research in areas like quantum physics and the study of chaotic systems. The seemingly unpredictable nature of prime distribution has sparked interest in exploring similar patterns in other complex systems.
Frequently Asked Questions (FAQ)
-
Are there infinitely many prime numbers? Yes, this is a fundamental theorem in number theory proven by Euclid over 2000 years ago. His proof uses a clever argument by contradiction.
-
What is the largest known prime number? The largest known prime number is constantly being updated as more powerful computers are employed in the search. These numbers are typically Mersenne primes (primes of the form 2<sup>p</sup> - 1, where p is also a prime number).
-
How are prime numbers used in hashing algorithms? Prime numbers are often used as the size of a hash table to minimize collisions. A prime number helps distribute keys more evenly across the table, leading to faster lookups and insertions.
-
Is there a formula to generate all prime numbers? There's no simple, closed-form formula to generate all prime numbers. While some formulas can generate sequences containing many primes, none generate only primes and are efficient for generating arbitrarily large primes.
Conclusion: The Enduring Mystery and Importance of Prime Numbers
The numbers 2, 3, 5, 7, and 11, seemingly simple at first glance, represent the gateway to a vast and intricate mathematical landscape. Their seemingly random distribution yet underlying order, coupled with their crucial role in modern cryptography and numerous other fields, underscores their profound importance. The ongoing research and exploration surrounding prime numbers highlight their enduring mystery and continuing relevance in both pure and applied mathematics. From securing our online transactions to advancing our understanding of the universe's fundamental laws, the seemingly simple prime numbers continue to shape our world in ways we are only beginning to fully appreciate. Their study is a testament to the power of human curiosity and the beauty of mathematical discovery. Further exploration into the world of prime numbers promises exciting discoveries and a deeper understanding of the intricate fabric of mathematics.
Latest Posts
Latest Posts
-
Convert 0 75 To A Fraction
Sep 14, 2025
-
Simplest Radical Form Of 48
Sep 14, 2025
-
Lcd Of 7 And 9
Sep 14, 2025
-
Sin 60 As A Fraction
Sep 14, 2025
-
What Shape Has 20 Sides
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 3 5 7 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.