19/6 As A Mixed Number
keralas
Sep 17, 2025 · 6 min read
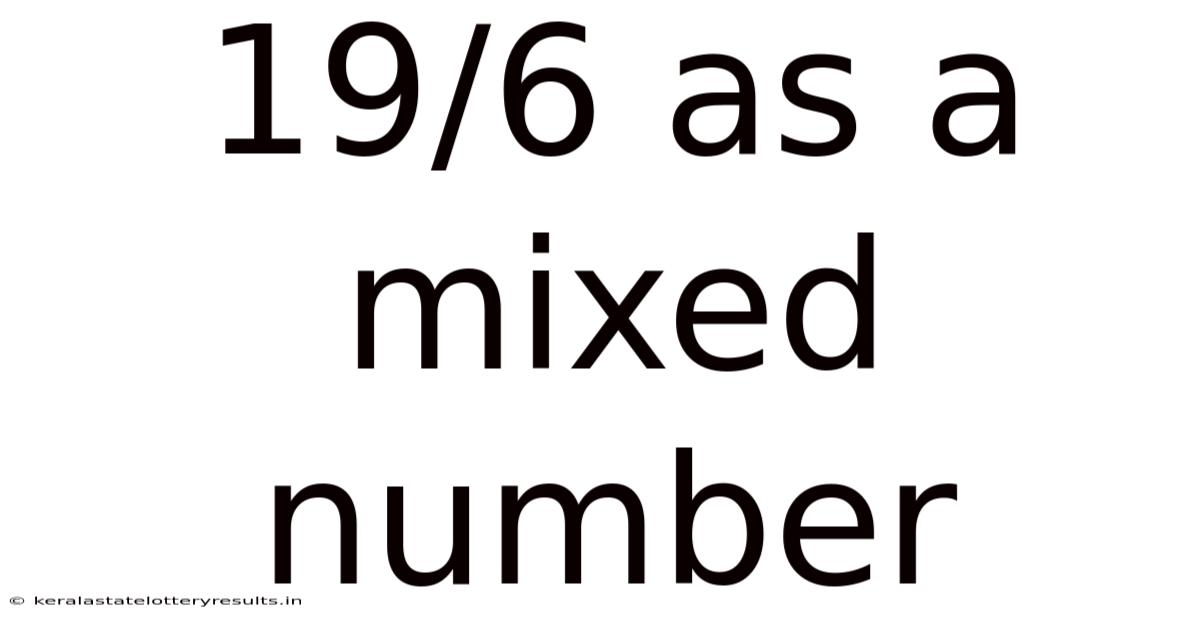
Table of Contents
Understanding 19/6 as a Mixed Number: A Comprehensive Guide
The fraction 19/6 represents nineteen sixths. While perfectly valid in its improper fraction form, it's often more intuitive and easier to visualize as a mixed number. This article will comprehensively explain what a mixed number is, how to convert 19/6 into a mixed number, the underlying mathematical principles involved, and answer frequently asked questions. We'll explore this concept in depth, suitable for students of various mathematical backgrounds.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator (the top number) smaller than the denominator (the bottom number). For example, 1 ½, 3 ¼, and 7 ⅛ are all mixed numbers. They represent quantities greater than one whole unit. Mixed numbers are particularly useful when dealing with real-world problems involving quantities that are not whole numbers. Imagine you have three pizzas, each cut into six slices, and you've already eaten 19 slices. Representing this as 19/6 slices isn't as immediately clear as representing it as a mixed number showing the whole pizzas consumed plus the remaining slices.
Converting 19/6 to a Mixed Number: A Step-by-Step Guide
The conversion process is straightforward and involves division. Here's how to convert the improper fraction 19/6 into a mixed number:
Step 1: Divide the Numerator by the Denominator
Divide the numerator (19) by the denominator (6).
19 ÷ 6 = 3 with a remainder of 1
Step 2: Identify the Whole Number and the Remainder
The quotient (the result of the division) becomes the whole number part of the mixed number. The remainder becomes the numerator of the fractional part.
- Whole Number: 3
- Remainder: 1
Step 3: Construct the Mixed Number
The whole number is written to the left of the fractional part, with the remainder as the numerator and the original denominator as the denominator.
Therefore, 19/6 as a mixed number is 3 1/6.
This means that 19/6 represents three whole units and one-sixth of another unit.
Visualizing the Conversion
Imagine you have 19 identical objects, and you want to group them into sets of 6. You'll be able to create three complete sets (3 x 6 = 18 objects) with one object remaining. This remaining object represents the fractional part (1/6). Hence, you have 3 complete sets and 1/6 of a set, perfectly mirroring the mixed number 3 1/6.
The Mathematical Principle Behind the Conversion
The conversion from an improper fraction to a mixed number relies on the fundamental principle of equivalent fractions and the concept of division. We are essentially decomposing the improper fraction into a sum of whole numbers and a proper fraction.
Let's break down 19/6 using this principle:
19/6 = (18/6) + (1/6) = 3 + 1/6 = 3 1/6
We've separated the fraction into two parts: a fraction that simplifies to a whole number (18/6 = 3) and a proper fraction (1/6). This clearly shows the mathematical basis for the conversion.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This is useful for performing calculations involving mixed numbers. Let's convert 3 1/6 back to an improper fraction:
Step 1: Multiply the Whole Number by the Denominator
Multiply the whole number (3) by the denominator (6): 3 x 6 = 18
Step 2: Add the Numerator
Add the result from Step 1 to the numerator (1): 18 + 1 = 19
Step 3: Write the Result Over the Original Denominator
Use the sum from Step 2 as the new numerator and keep the original denominator: 19/6
This confirms that 3 1/6 and 19/6 are equivalent representations of the same quantity.
Real-World Applications of Mixed Numbers
Mixed numbers are invaluable in everyday life, appearing frequently in various contexts:
- Cooking and Baking: Recipes often require fractional amounts of ingredients, frequently expressed as mixed numbers (e.g., 2 ½ cups of flour).
- Measurement: Measuring lengths, weights, and volumes often results in mixed numbers (e.g., 5 ¾ inches).
- Time: We commonly use mixed numbers to represent time (e.g., 1 ½ hours).
- Construction and Engineering: Precise measurements in construction and engineering often involve mixed numbers to represent dimensions and quantities.
Why Use Mixed Numbers?
While improper fractions are mathematically accurate, mixed numbers offer several advantages:
- Intuitive Understanding: Mixed numbers are more easily grasped intuitively. It's easier to visualize 3 1/6 pizzas than 19/6 pizzas.
- Simplified Calculations: In some contexts, mixed numbers can simplify calculations, particularly when adding or subtracting fractions.
- Clearer Communication: Mixed numbers communicate quantities more clearly in everyday situations.
Frequently Asked Questions (FAQ)
Q1: Can every improper fraction be converted into a mixed number?
Yes, every improper fraction can be converted into a mixed number. This is because the numerator is always larger than the denominator in an improper fraction, guaranteeing that a whole number portion will always exist after division.
Q2: What if the remainder is zero after division?
If the remainder is zero, it means the improper fraction is actually a whole number. For example, 12/3 = 4, which is already a whole number. In this case, no fractional part exists in the mixed number representation.
Q3: Is it always necessary to convert improper fractions to mixed numbers?
Not necessarily. The choice between using an improper fraction or a mixed number depends on the context. For some calculations (like multiplication and division of fractions), improper fractions are often more convenient. However, for representing quantities in everyday contexts, mixed numbers are often preferred for their clarity.
Q4: How do I compare mixed numbers?
To compare mixed numbers, first compare the whole number parts. If the whole number parts are different, the larger whole number corresponds to the larger mixed number. If the whole number parts are the same, then compare the fractional parts.
Q5: Can I convert decimal numbers into mixed numbers?
Yes, you can. First, convert the decimal number into a fraction, then convert the fraction into a mixed number (if it's an improper fraction).
Conclusion
Understanding the conversion between improper fractions and mixed numbers is a crucial skill in mathematics. This ability is not only essential for solving mathematical problems but also for applying mathematical concepts to real-world situations. By mastering this concept, you’ll be better equipped to handle a wide range of mathematical tasks and everyday challenges involving fractional quantities. Remember the key steps: divide the numerator by the denominator, identify the whole number and remainder, and construct the mixed number. Practice converting both ways – from improper fractions to mixed numbers and vice versa – to solidify your understanding. Through consistent practice and application, you will develop a deep and confident grasp of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Linear Equations Real World Examples
Sep 17, 2025
-
Gcf Of 18 And 63
Sep 17, 2025
-
Prime And Composite Numbers Chart
Sep 17, 2025
-
Area Of A Isosceles Trapezoid
Sep 17, 2025
-
Gcf Of 63 And 54
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 19/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.