15 Percent In A Fraction
keralas
Sep 14, 2025 · 6 min read
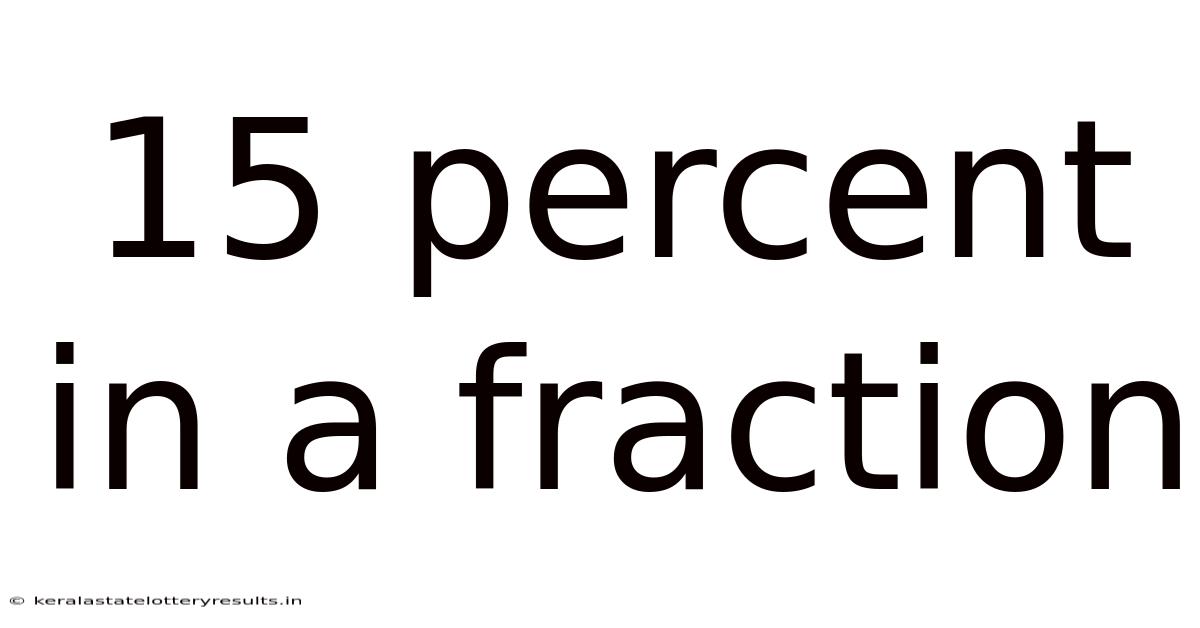
Table of Contents
15 Percent: Understanding, Representing, and Applying This Common Percentage
15 percent. We encounter this figure frequently – in sales discounts, interest rates, tax calculations, and countless other applications. Understanding how to represent 15% as a fraction, and working with it in various contexts, is a fundamental skill for navigating everyday life and more advanced mathematical concepts. This article will provide a comprehensive guide, explaining not only how to convert 15% to a fraction but also exploring its applications and implications across different fields.
Understanding Percentages and Fractions
Before diving into the specifics of 15%, let's briefly review the relationship between percentages and fractions. A percentage is simply a way of expressing a fraction out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be directly converted into a fraction by writing the percentage number as the numerator and 100 as the denominator.
For example:
- 50% = 50/100
- 25% = 25/100
- 75% = 75/100
This fundamental understanding forms the bedrock of converting 15% into its fractional equivalent.
Converting 15% to a Fraction: The Step-by-Step Process
Converting 15% to a fraction is straightforward:
-
Write the percentage as a fraction: 15% becomes 15/100. This directly reflects the definition of percentage – 15 parts out of 100.
-
Simplify the fraction: The fraction 15/100 can be simplified by finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (100). The GCD of 15 and 100 is 5.
-
Divide both the numerator and the denominator by the GCD: Dividing both 15 and 100 by 5 gives us 3/20.
Therefore, 15% expressed as a fraction in its simplest form is 3/20.
Understanding the Significance of Simplifying Fractions
Simplifying fractions is crucial for several reasons:
-
Clarity: A simplified fraction is easier to understand and interpret than a more complex one. 3/20 is significantly clearer than 15/100.
-
Calculations: Simplified fractions make calculations involving multiplication and division much simpler. Working with 3/20 is considerably less cumbersome than working with 15/100, especially when dealing with more complex calculations.
-
Comparisons: Comparing simplified fractions is easier. For instance, comparing 3/20 to other fractions will be simpler than comparing 15/100.
Applications of 15% in Real-World Scenarios
The application of 15% spans various domains:
-
Sales and Discounts: A 15% discount on a $100 item means a reduction of $15 (15/100 * $100 = $15). This is a common scenario in retail sales, online shopping, and promotional offers.
-
Taxes: Sales tax, Value Added Tax (VAT), and other taxes often involve percentages. Understanding how to calculate 15% tax is essential for budgeting and financial planning.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are frequently expressed as percentages. A 15% interest rate on a loan means you'll pay 15% of the principal amount as interest over a specific period.
-
Statistics and Probability: In statistical analysis, 15% might represent a certain proportion of a population or a probability of an event occurring.
-
Financial Modeling: In financial modeling, 15% could represent a growth rate, discount rate, or margin in various financial projections and analyses.
-
Data Analysis: In data analysis, 15% might represent a particular segment of data, requiring further examination and interpretation.
Working with 15% in Different Mathematical Operations
Let's explore how to work with 15% (or 3/20) in different mathematical operations:
-
Addition: Adding 15% to a number means increasing it by 15%. For example, adding 15% to 50 is equivalent to 50 + (15/100 * 50) = 57.5
-
Subtraction: Subtracting 15% from a number means decreasing it by 15%. For example, subtracting 15% from 100 is equivalent to 100 - (15/100 * 100) = 85.
-
Multiplication: Multiplying a number by 15% yields 15% of that number. For example, 15% of 200 is (15/100 * 200) = 30.
-
Division: Dividing a number by 15% is less common but can be encountered in specific applications. For example, if 30 represents 15% of a total, the total would be 30 / (15/100) = 200.
Converting Fractions Back to Percentages
The reverse process—converting a fraction back to a percentage—is equally important. To do this, divide the numerator by the denominator and then multiply the result by 100. For instance, converting 3/20 back to a percentage:
(3/20) * 100 = 15%
This demonstrates the interchangeable nature of percentages and fractions.
Advanced Applications and Concepts
Beyond basic calculations, understanding 15% plays a role in more advanced concepts:
-
Compound Interest: Compound interest calculations involve repeatedly applying a percentage (like 15%) to an accumulating balance, leading to exponential growth.
-
Growth Rates: In economics and finance, 15% might represent a growth rate of an investment, a company's revenue, or an economy's GDP. Understanding how this rate impacts future projections is crucial.
-
Proportional Reasoning: The ability to work with percentages like 15% is a fundamental aspect of proportional reasoning—a critical skill used extensively in problem-solving and decision-making across many disciplines.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 15%?
A: The simplest form of 15% as a fraction is 3/20.
Q: How do I calculate 15% of a number?
A: Multiply the number by 0.15 (the decimal equivalent of 15%) or by the fraction 3/20.
Q: Can I use a calculator to work with 15%?
A: Yes, calculators are helpful for working with percentages. You can either use the percentage function directly or convert the percentage to a decimal and perform the calculation.
Q: What if I need to work with 15% in a more complex equation?
A: The same principles apply—convert 15% to its fractional or decimal equivalent (3/20 or 0.15) and incorporate it into your calculations. Understanding the order of operations (PEMDAS/BODMAS) will be crucial for accurate results.
Q: Are there any online tools to help with percentage calculations?
A: While this article doesn't endorse specific external sites, many online calculators and educational resources are available to assist with percentage calculations.
Conclusion: Mastering the Power of 15%
Understanding and working with 15% – whether as a percentage, decimal, or fraction – is a crucial skill applicable across various aspects of life. From everyday shopping to complex financial modeling, the ability to confidently manipulate this common percentage equips you with a valuable tool for navigating numerical challenges. By mastering the conversion between percentages and fractions and applying the principles outlined in this article, you can confidently tackle a wide range of problems involving this frequently encountered numerical concept. Remember, the key lies in understanding the underlying principles and applying them consistently. With practice, working with percentages like 15% will become second nature.
Latest Posts
Latest Posts
-
Simplified Square Root Of 20
Sep 14, 2025
-
How Do You Spell 97
Sep 14, 2025
-
Gcf For 6 And 8
Sep 14, 2025
-
8 Divided By 3 Fraction
Sep 14, 2025
-
Gcf For 40 And 48
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.