15 Of What Is 12
keralas
Sep 16, 2025 · 5 min read
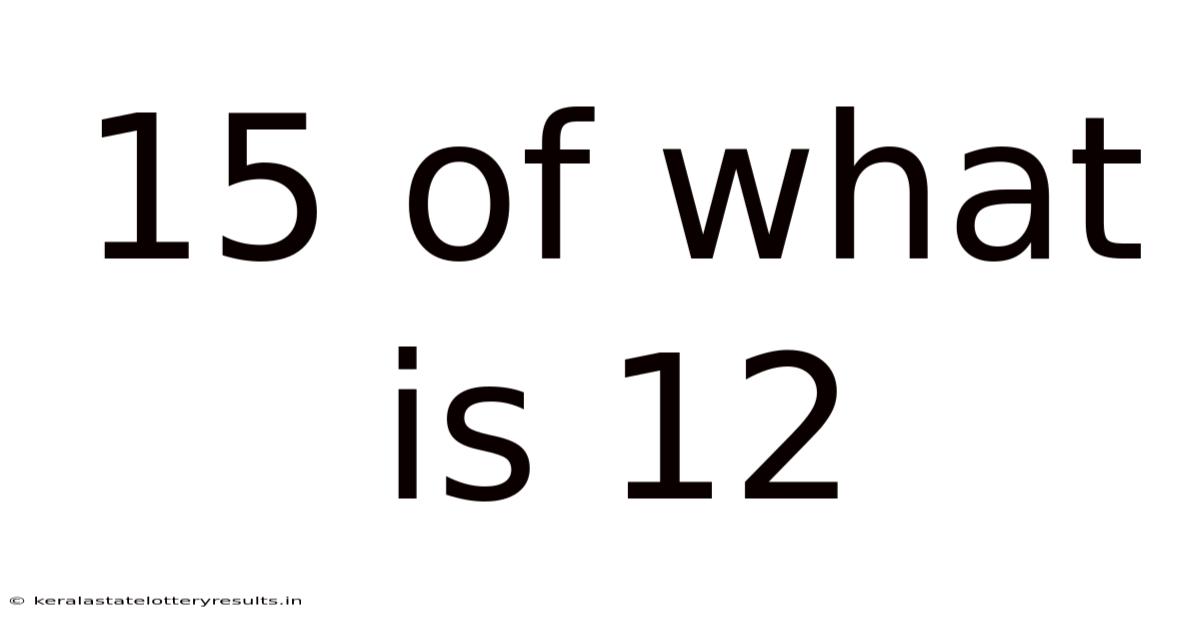
Table of Contents
Unveiling the Mystery: 15 of What is 12? A Deep Dive into Fractions, Ratios, and Proportions
Understanding fractions, ratios, and proportions is fundamental to mathematics and countless real-world applications. This article delves into the seemingly simple question, "15 of what is 12?", exploring the underlying mathematical concepts and demonstrating various methods for solving similar problems. We will move beyond a simple answer to build a strong understanding of the principles involved, making you confident in tackling more complex proportional reasoning problems.
Understanding the Problem: Deconstructing "15 of What is 12?"
The phrase "15 of what is 12" represents a proportional relationship. It can be interpreted as: a certain fraction (15/x, where x is the unknown quantity) of a whole number (x) equals 12. This is a classic example of a problem that can be solved using several mathematical approaches, including setting up an equation, using cross-multiplication, or employing the concept of ratios. We'll explore each method in detail.
Method 1: Setting Up an Equation
The most straightforward approach involves translating the problem into an algebraic equation. "15 of what is 12" can be written as:
(15/x) * x = 12
This equation expresses the relationship between the fraction (15/x), the unknown whole (x), and the result (12). However, this particular equation simplifies to 15 = 12, which is a contradiction. This shows that the initial phrasing "15 of what is 12" is slightly ambiguous and better expressed as a percentage or a different fraction. Let's re-interpret the problem to create solvable equations.
Reinterpreting the Question: Let's assume the question meant to ask: "15% of what number is 12?" or "What number is 15/x of a number such that this number equals 12?"
Scenario 1: 15% of what number is 12?
This can be written as:
0.15 * x = 12
To solve for x, we divide both sides of the equation by 0.15:
x = 12 / 0.15 = 80
Therefore, 15% of 80 is 12.
Scenario 2: Solving for the proportion using a different fraction: Let's assume the question intended to use a fraction other than 15%, for example, that 15 is the numerator of an unknown fraction and 12 is the result when this fraction of x is taken. So, let's try to reformulate the question as: "15/x of what is 12?".
This translates to:
(15/x) * x = 12
This simplifies to: 15 =12 which isn't possible.
Let's reconsider the phrasing. A more accurate way to represent this would be : "12 is 15/x of what number?"
This translates to the equation:
12 = (15/x) * y (where y represents the unknown number)
We can rearrange the equation to solve for y:
y = (12 * x) / 15
To solve for y, we need a value for x. Let's assume that 15/x represents a fraction such as 15/25, 15/50 or 15/100 (15%).
If 15/x = 15/25 = 3/5:
12 = (3/5) * y y = (12 * 5) / 3 = 20
If 15/x = 15/100 (or 15%): we've already solved this in scenario 1, y = 80
This highlights the importance of precise phrasing when dealing with mathematical problems. The original statement was too ambiguous to solve directly.
Method 2: Using Cross-Multiplication (Proportions)
The problem can also be approached using proportions. A proportion is a statement of equality between two ratios. Let's assume the question is asking, “15% of what number is 12?” We can set up a proportion:
15/100 = 12/x
Cross-multiplying, we get:
15x = 1200
Dividing both sides by 15:
x = 80
This confirms our earlier result that 15% of 80 is 12. This method is visually intuitive and helpful for understanding proportional relationships.
Method 3: Understanding Ratios
The core of this problem lies in understanding ratios. A ratio compares two quantities. In our revised interpretation ("15% of what number is 12?"), the ratio is 15:100, representing the percentage. We can express this ratio as a fraction (15/100). This fraction is then applied to the unknown quantity (x) to obtain 12. Therefore, we can use the equation:
(15/100) * x = 12
This is the same equation we solved in Method 1 and Method 2 and yields the same answer, x = 80.
Expanding the Concept: Real-World Applications of Proportional Reasoning
Proportional reasoning is vital in various real-world scenarios:
- Cooking: Scaling recipes up or down requires proportional adjustments to ingredient quantities.
- Finance: Calculating interest, discounts, and taxes all rely on proportional relationships.
- Science: Many scientific formulas and experiments involve proportional relationships between variables.
- Engineering: Designing structures and machines requires precise calculations based on proportional relationships.
- Mapping: Maps use scale to represent geographical areas, employing a proportional relationship between map distance and actual distance.
Frequently Asked Questions (FAQ)
Q: What if the problem was phrased differently? The ambiguity of the original problem highlights the importance of clear communication in mathematics. A more precise question would avoid confusion.
Q: Can this be solved using other methods? Yes, advanced mathematical techniques like linear algebra could be applied, but for this particular problem, the methods described above are the most efficient and conceptually clear.
Q: Why is understanding fractions and ratios important? Fractions and ratios form the basis of many mathematical concepts. Mastering them builds a strong foundation for algebra, calculus, and more advanced mathematical disciplines.
Conclusion: Beyond the Numbers
Solving "15 of what is 12?" (re-interpreted for clarity) isn't just about finding the answer (80). It's about understanding the underlying principles of fractions, ratios, proportions, and the importance of precise mathematical language. By mastering these concepts, you gain a powerful toolset applicable across various fields, improving your problem-solving skills and analytical thinking abilities. The journey from a seemingly simple question to a deep understanding of proportional reasoning is a testament to the richness and interconnectedness of mathematics. Remember, the ability to translate word problems into mathematical equations is a crucial skill – practice makes perfect! Keep exploring and expanding your mathematical knowledge; the rewards are immeasurable.
Latest Posts
Latest Posts
-
Gcf Of 27 And 9
Sep 16, 2025
-
What Is 10 Of 30000
Sep 16, 2025
-
Gcf Of 18 And 72
Sep 16, 2025
-
Gcf Of 40 And 28
Sep 16, 2025
-
One Thousand And Eight Hundred
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 15 Of What Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.