15/4 As A Mixed Number
keralas
Sep 15, 2025 · 5 min read
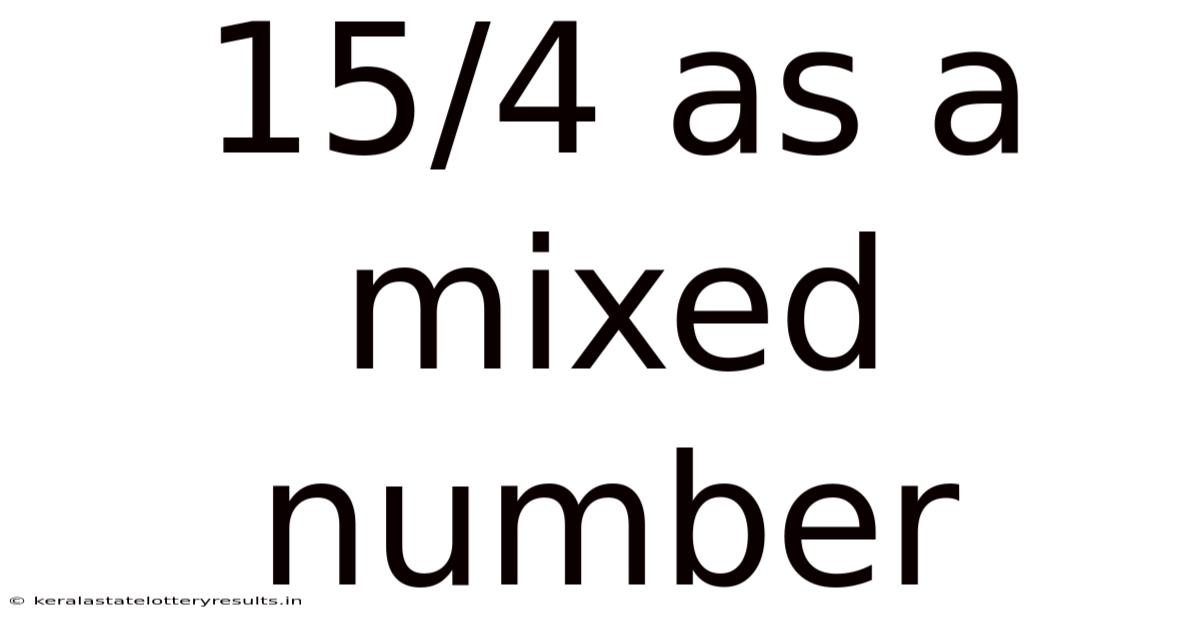
Table of Contents
Understanding 15/4 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 15/4 might appear straightforward at first glance, but it holds a wealth of mathematical concepts within its concise form. This article will delve deep into understanding 15/4, not just as an improper fraction, but as a mixed number, exploring its conversion, applications, and related mathematical principles. We'll also address common questions and misconceptions, providing a comprehensive understanding suitable for students and anyone seeking to strengthen their grasp of fractions.
What is a Mixed Number?
Before tackling 15/4 specifically, let's establish a firm understanding of mixed numbers. A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number), like 1/2 or 3/4. A mixed number represents a quantity greater than one. For example, 2 1/2 represents two whole units and an additional half.
Converting 15/4 to a Mixed Number: A Step-by-Step Approach
The fraction 15/4 is an improper fraction because the numerator (15) is larger than the denominator (4). To convert it to a mixed number, we need to determine how many times 4 goes into 15 and what the remainder is.
Step 1: Perform the Division
Divide the numerator (15) by the denominator (4):
15 ÷ 4 = 3 with a remainder of 3.
Step 2: Interpret the Results
- The quotient (3) becomes the whole number part of the mixed number.
- The remainder (3) becomes the numerator of the fractional part.
- The denominator remains the same (4).
Step 3: Write the Mixed Number
Therefore, the mixed number equivalent of 15/4 is 3 3/4. This means that 15/4 represents three whole units and three-quarters of another unit.
Visualizing 15/4
Imagine you have 15 equally sized pieces of a pizza. If each pizza is cut into 4 slices, how many whole pizzas do you have?
You can make 3 complete pizzas using 12 slices (4 slices/pizza * 3 pizzas = 12 slices). You'll have 3 slices left over, which is 3/4 of a pizza. This visually demonstrates why 15/4 is equivalent to 3 3/4.
The Importance of Understanding Mixed Numbers
Converting improper fractions to mixed numbers is crucial for several reasons:
- Clarity and Interpretation: Mixed numbers are easier to visualize and understand than improper fractions. Saying "I ate 3 3/4 pizzas" is clearer than saying "I ate 15/4 pizzas."
- Real-World Applications: Many real-world measurements and quantities are expressed using mixed numbers, such as 2 1/2 inches or 1 3/4 cups.
- Mathematical Operations: While addition and subtraction can be performed with improper fractions, it's often easier and less error-prone to work with mixed numbers, particularly when dealing with larger fractions.
Converting Mixed Numbers back to Improper Fractions
It's equally important to be able to convert mixed numbers back into improper fractions. This is necessary for certain mathematical operations, especially multiplication and division of fractions.
To convert 3 3/4 back to an improper fraction:
Step 1: Multiply the whole number by the denominator.
3 * 4 = 12
Step 2: Add the numerator.
12 + 3 = 15
Step 3: Keep the same denominator.
The improper fraction is therefore 15/4.
Further Applications and Extensions
The concept of converting between improper fractions and mixed numbers extends to more complex scenarios:
- Working with larger numbers: The same principles apply when dealing with significantly larger numerators and denominators. The division process might require more steps, but the core methodology remains consistent.
- Decimals and Fractions: Mixed numbers can be readily converted to decimals and vice-versa, providing a bridge between different numerical representations. For example, 3 3/4 is equivalent to 3.75.
- Algebraic Expressions: Understanding mixed numbers is foundational for tackling more advanced algebraic expressions involving fractions.
Common Mistakes and How to Avoid Them
- Incorrect Division: Ensure you perform the division correctly. Mistakes in division will lead to an incorrect mixed number. Double-check your calculations.
- Ignoring the Remainder: The remainder is crucial! It forms the numerator of the fractional part of the mixed number. Don't forget to include it.
- Incorrect Denominator: The denominator in the mixed number always remains the same as the denominator in the improper fraction.
Frequently Asked Questions (FAQ)
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, every improper fraction can be converted to a mixed number.
Q: Is there only one way to represent a given quantity as a mixed number?
A: No, there are multiple ways to represent a quantity as a mixed number. A fraction like 15/4 can only be reduced in the form of 3 3/4, however, if we had a fraction like 20/6, the mixed number could be written as 3 2/6 or 3 1/3
Q: Why is it important to learn about mixed numbers?
A: Understanding mixed numbers improves mathematical fluency, allows for easier comprehension of real-world quantities, and simplifies operations with fractions.
Q: What happens if the numerator is exactly divisible by the denominator?
A: If the numerator is exactly divisible by the denominator, the result will be a whole number, and the fractional part of the mixed number will be zero. For example, 8/4 is equal to 2.
Conclusion
Understanding the conversion between improper fractions and mixed numbers is a cornerstone of fractional arithmetic. This comprehensive guide has provided a step-by-step approach to converting 15/4 to its mixed number equivalent, 3 3/4, exploring its visual representation, and highlighting practical applications. Mastering this fundamental concept unlocks a deeper understanding of fractions and lays a strong foundation for tackling more advanced mathematical problems. Remember to practice regularly and always double-check your calculations to build confidence and accuracy.
Latest Posts
Latest Posts
-
40 Degrees Centigrade In Fahrenheit
Sep 15, 2025
-
Lateral And Surface Area Formulas
Sep 15, 2025
-
How Many Weeks Is 4months
Sep 15, 2025
-
What Is A Factor Form
Sep 15, 2025
-
5 12 In Decimal Form
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 15/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.