1 Divided By 1 3
keralas
Sep 15, 2025 · 5 min read
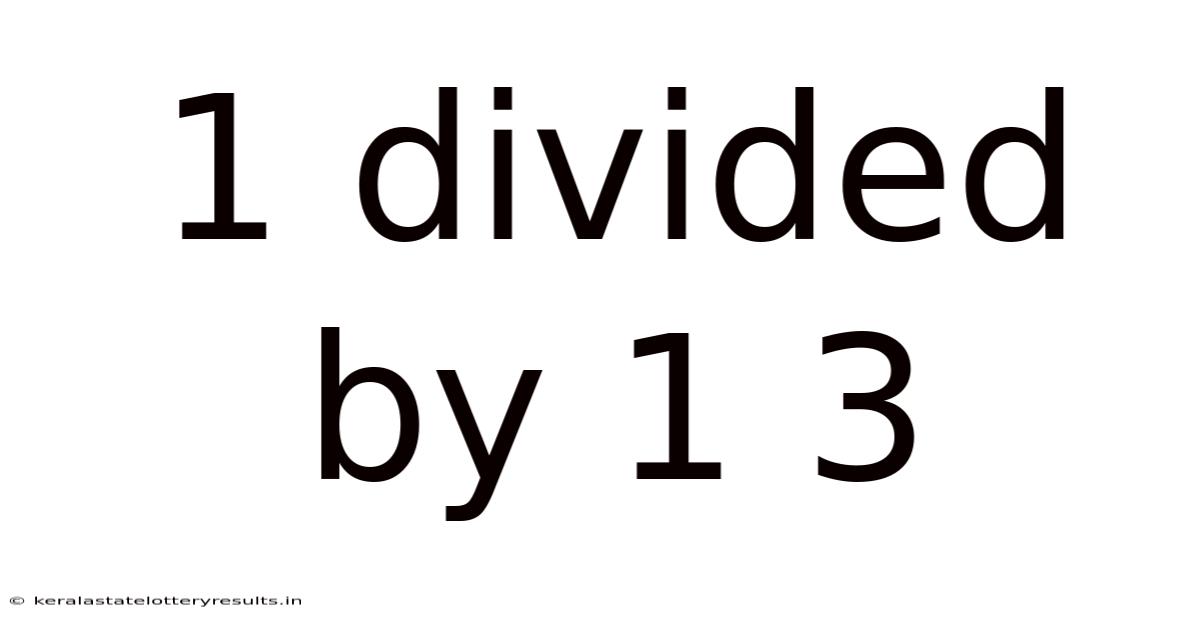
Table of Contents
Decoding 1 Divided by 1 1/3: A Deep Dive into Fractions and Division
Many of us encounter fractions in our daily lives, from splitting a pizza with friends to calculating recipe ingredients. Understanding how to divide by fractions, particularly a mixed number like 1 1/3, is a fundamental skill with far-reaching applications. This article will provide a comprehensive explanation of how to solve 1 divided by 1 1/3, exploring the underlying mathematical principles and offering various approaches to ensure a solid grasp of the concept. We'll also tackle common misconceptions and frequently asked questions to leave you with a complete understanding of this seemingly simple yet important calculation.
Understanding the Problem: 1 ÷ 1 1/3
The problem, 1 ÷ 1 1/3, asks us to determine how many times 1 1/3 fits into 1. This seemingly counterintuitive question highlights the importance of understanding fraction division. At first glance, it might seem like the answer is less than 1, since the divisor (1 1/3) is larger than the dividend (1). However, we will see that the process of division with fractions leads to a surprising yet mathematically accurate result.
Method 1: Converting to Improper Fractions
The most common and generally preferred method involves converting the mixed number (1 1/3) into an improper fraction. This simplifies the division process significantly.
Step 1: Convert the Mixed Number to an Improper Fraction:
A mixed number like 1 1/3 represents a whole number (1) plus a fraction (1/3). To convert it to an improper fraction, we multiply the whole number by the denominator and add the numerator, keeping the same denominator.
1 1/3 = (1 * 3 + 1) / 3 = 4/3
Step 2: Rewrite the Division Problem:
Now our problem becomes 1 ÷ 4/3. Remember that dividing by a fraction is the same as multiplying by its reciprocal.
Step 3: Find the Reciprocal:
The reciprocal of a fraction is obtained by switching the numerator and the denominator. The reciprocal of 4/3 is 3/4.
Step 4: Multiply:
Our problem is now rewritten as 1 * 3/4. Multiplying a whole number by a fraction is straightforward: multiply the whole number by the numerator and keep the denominator the same.
1 * 3/4 = 3/4
Therefore, 1 divided by 1 1/3 equals 3/4.
Method 2: Using Long Division with Fractions
While the improper fraction method is more efficient, understanding the long division approach offers a deeper insight into the process. This method is less practical for this specific problem but demonstrates a valuable skill applicable to more complex scenarios.
Step 1: Express 1 as a fraction:
We can rewrite 1 as 3/3, maintaining the same value but using a common denominator with the divisor (1 1/3).
Step 2: Perform Long Division:
We now have 3/3 divided by 4/3. Imagine this as asking "how many times does 4/3 go into 3/3?". Long division with fractions is conceptually similar to long division with whole numbers. However, instead of subtracting repeatedly, we multiply by the reciprocal of the divisor.
In essence we are asking: (3/3) / (4/3) = (3/3) * (3/4) = 9/12
Step 3: Simplify:
The fraction 9/12 can be simplified by dividing both numerator and denominator by their greatest common divisor, which is 3.
9/12 = (9 ÷ 3) / (12 ÷ 3) = 3/4
Again, we arrive at the answer: 3/4.
Method 3: Visual Representation
Visualizing the problem can aid in understanding. Imagine a pizza. One whole pizza represents the dividend (1). Now, imagine dividing this pizza into portions of 1 1/3. You can't perfectly fit a full 1 1/3 pizza slice into one pizza, which is why we get a fractional answer.
To visualize this more precisely, consider cutting the pizza into 12 equal slices. One whole pizza would then consist of 12/12 slices. A portion of 1 1/3 is equivalent to (12/12)/(4/3) or 4 slices. One whole pizza would consist of three 4/3 slices (4/3+4/3+4/3). Hence, one whole pizza has 3/4 of 1 1/3 portions.
The Mathematical Principle Behind Fraction Division
The core concept behind dividing by a fraction rests on the relationship between multiplication and division. Dividing by a fraction is equivalent to multiplying by its reciprocal. This is because division can be seen as the inverse operation of multiplication. When we divide by a fraction, we're essentially asking, "How many times does this fraction fit into the whole number (or another fraction)?" The reciprocal allows us to frame this question as a multiplication problem, simplifying the calculation process.
Common Misconceptions
A common mistake is to directly divide the numerators and the denominators without converting to improper fractions. This leads to incorrect results. Always remember to convert mixed numbers to improper fractions before performing division.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this problem using decimals? A: Yes, you can convert the fractions to decimals first. 1 1/3 is approximately 1.333... Dividing 1 by 1.333... will also yield approximately 0.75, which is equivalent to 3/4. However, using fractions offers greater precision, especially when dealing with repeating decimals.
-
Q: What if the dividend was also a fraction? A: The process remains the same. You would convert both fractions to improper fractions and then multiply the first by the reciprocal of the second.
-
Q: Are there other methods to solve this? A: While the methods discussed are the most common and efficient, alternative methods exist depending on the complexity of the problem, but these are generally less intuitive.
-
Q: What are some real-world applications of this concept? A: Dividing by fractions has countless practical applications, from cooking (adjusting recipes) to construction (measuring materials) to finance (calculating proportions).
Conclusion
Understanding how to solve 1 divided by 1 1/3, and more generally, how to divide by fractions, is crucial for anyone seeking a solid foundation in mathematics. Mastering this skill not only helps solve specific problems but also provides a deeper understanding of the underlying mathematical principles. By employing the methods explained here, and by understanding the concepts behind fraction division, you'll develop the confidence and skills to tackle more complex mathematical challenges. Remember, practice is key to mastering fractions and their operations. Consistent effort will build your understanding and make these calculations second nature.
Latest Posts
Latest Posts
-
Midpoint Formula Elasticity Of Demand
Sep 15, 2025
-
X 2 Y 2 1
Sep 15, 2025
-
1 4 Mile In Ft
Sep 15, 2025
-
Simplify X 2 1 2
Sep 15, 2025
-
Is 81 A Perfect Square
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.